處理複雜流體問題的統御方程式為偏微分方程,由於多數偏微分方程沒有解析解,所以多半是用電腦求解,過程中先將物理問題離散後,再來求得解析解。因此,今天將會以微處理器散熱為例來說明CFD離散程序。
CFD離散程序總覽
離散程序主要包含三個步驟,分別是決定幾何與物理模型、物理區域離散與方程式離散。而幾何與物理模型之所以與離散相關,是因為求解問題的幾何形狀與問題種類會影響後面步驟。
從前幾碗雞湯的統御方程式推導可知推導流程都是基於形狀規則的控制體積來推導,但真實世界的問題多半是求解不規則形狀的模型,像是風扇或散熱鰭片等等。
為了要讓統御方程式可以套用不同幾何模型,求解過程中會將不規則形狀的模型切成數個若干規則形狀的元素,如圖1。透過求解各個元素的數值解,進而找到模型整體變數值分布狀況,如溫度分布、速度分布等等。
由於不同物理問題的統御方程式不同,離散方程式也會有所差別,所以除了幾何區域以外,還需要決定物理問題種類。底下將會用簡化微處理器的散熱問題來說明CFD離散程序。
Step1: 幾何與物理模型
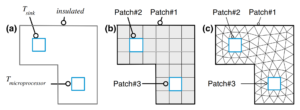
圖2展示一個微處理器的二維模型,透過銅製基板擴散的熱能會被散熱器吸收,進而降低微處理器溫度。由於元件間的幾何關係在設計過程中決定,故下一步要來決定此問題的物理模型。
由於整體溫度分布狀況僅與熱傳相關,故使用能量守恆方程式作為求解用的物理模型,不需連續方程式與Navier-Stokes方程式。簡化後的能量守恆方程式如式(1)所示。
-\triangledown \cdot (k\triangledown T)=\dot{q} - (1)
其中k為銅製基板的熱傳導率,\dot{q}則是熱源每單位體積吸收或釋放的熱能。而銅製基板數個邊緣套用隔熱邊界條件。
Step2: 計算區域離散
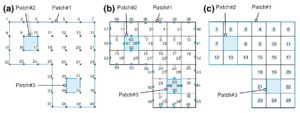
確定幾何與物理模型後,接著就是計算區域的離散化。前面提到為了要讓統御方程式套用不同幾何模型,會將不規則形狀的模型切成數個若干規則形狀的元素來求解,此過程又稱為網格(Mesh)劃分,如圖3。而圖3(b)與(c)的計算區域被劃分成數個正方形網格或是三角形網格。
Step3: 方程式離散
方程式離散主要是將偏微分方程轉換成線性代數方程,而這樣做能夠讓我們用電腦求出近似解,形式如式(2)所示。其中a與T分別代表離散方程式係數與求解變數,下標C與F為當下求解網格編號與周遭網格編號。
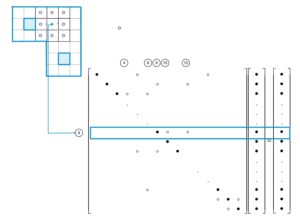
在後續求解過程中,將不同編號的元素代入離散後的線性代數方程,再把這些方程式組成待求解矩陣,就能使用演算法來求解,待求解矩陣示意可參照圖5。由於式(2)是整理過後的結果,單看式(2)可能會感到疑惑,故底下將會以微處理器問題來說明離散過程。
a_C T_C+\sum_{F \sim NB(C)} a_F T_F = b_c - (2)
了解離散方程式的基本概念後,接著來看看如何離散式(1)。首先我們可以將式(1)的偏微分方程表示成積分形式,如式(3)。基於散度定理(Divergence theorem),可以將元素內部變化表示成周遭曲面的通量變化,如式(4)。
-\iint_{V_C} \triangledown \cdot (k \triangledown T)dV = \iint_{V_C} \dot{q}dV - (3)
-\int_{S_C}(k \triangledown T)d\mathbf{S}= \dot{q}_C V_C - (4)
基於式(4)概念與離散網格,我們可以將式(4)中的面積分項近似成當下求解元素構成面的通量總和,如式(5)所示,其中下標f代表當下求解元素構成面的中心點,而式(6)為式(5)的展開式,網格編號關係可參照圖6。
-\sum_{f\sim nb(C)} (k \triangledown T)_f \cdot \mathbf{S}_f = \dot{q} Vc- (5)
-(k\triangledown T)_{f1} \cdot \mathbf{S}_{f1}-(k\triangledown T)_{f2} \cdot \mathbf{S}_{f2}-(k\triangledown T)_{f3} \cdot \mathbf{S}_{f3}-(k\triangledown T)_{f4} \cdot \mathbf{S}_{f4} = \dot{q}_C V_C- (6)
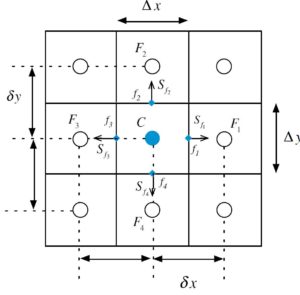
為了求解偏微分方程,需要用網格參數來表示式(6)中的溫度梯度與面法向量,以面F1為例的表示式如下列所示:
\mathbf{S}_{f1} = \triangle y_{f1} \mathbf{i}- (7)
\delta x_{f1} = x_{F1} - x_C - (8)
\triangledown T_{f1} = \left ( \frac{\partial T}{\partial x} \right )_{f1}\mathbf{i}+\left ( \frac{\partial T}{\partial y} \right )_{f1}\mathbf{j}- (9)
其中x_C為元素C的X座標,x_{f1}為元素F1的X座標,\triangle y_{f1} 為面f1面積,\mathbf{S}_{f1}為面f1的面法向量,\triangledown T_{f1}為面F1中心點的溫度梯度。
將式(7) – 式(9)代入式(6),可將f1相關項表示成下列式子。
\triangledown T_{f1} \cdot \mathbf{S}_{f1} = \left ( \frac{\partial T}{\partial x} \mathbf{i}+\frac{\partial T}{\partial y} \mathbf{j}\right )_{f1} \cdot \triangle y_{f1} \mathbf{i} = \left ( \frac{\partial T}{\partial x} \right )_{f1} \triangle y_{f1} - (10)
假設元素間的溫度變化為線性關係,式(10)中的偏微分梯度項可表示成式(11)。將式(11)代入式(10)後可以將-(k\triangledown T)_{f1} \cdot \mathbf{S}_{f1}表示成式(12),至此已經找出f1項與網格參數的關係。
\left ( \frac{\partial T}{\partial x} \right )_{f1}=\frac{T_{F1}-T_{C}}{\delta x_{f1}} - (11)
-(k\triangledown T)_{f1} \cdot \mathbf{S}_{f1} = a_{F1}(T_{F1} - T_C) - (12)
a_{F1} = -k\frac{\triangle y_{f1}}{\delta x_{f1}} - (13)
重複上述步驟,其他項也能得到同樣形式的係數表示項,因此式(6)最終可改寫成底下形式,如式(14)所示,至此也完整表示式(6)的離散方程式,將不同的元素編號代入後就能得到該元素離散方程式,並組成大型矩陣求解。
-\sum_{f \sim nb(C)} (k \triangledown T)_f \cdot \mathbf{S}_f = -(a_{F1}+a_{F2}+a_{F3}+a_{F4})T_C + a_{F1}T_{F1}+a_{F2}T_{F2}+a_{F3}T_{F3}+a_{F4}T_{F4} = \dot{q}_C V_C - (14)
主廚結語
此次跟各位概括介紹CFD求解的離散流程,雖然這些運算看起來有些複雜,但如果只是單純使用商業軟體,這些運算都已經寫在軟體內部,操作上並不會這麼可怕。如果對這方面資訊有興趣的話,可以追蹤科技雞湯臉書專頁,時刻更新消息!
參考資料
- F. Moukalled et al., The Finite Volume Method in Computational Fluid Dynamics, 2015
