(本文經Prof. Lorena A. Barba授權轉載翻譯自Prof. Lorena A. Barba的教材”12 Steps to Navier-Stokes”,原文鏈結請參照底下參考資料)
Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved BSD-3 license. (c) Lorena A. Barba, Gilbert F. Forsyth 2017. Thanks to NSF for support via CAREER award #1149784.
CFD Python:求解Navier-Stokes方程的12個步驟(1) CFD Python:求解Navier-Stokes方程的12個步驟(2) CFD Python:求解Navier-Stokes方程的12個步驟(3) CFD Python:求解Navier-Stokes方程的12個步驟(4) CFD Python:求解Navier-Stokes方程的12個步驟(5) CFD Python:求解Navier-Stokes方程的12個步驟(6) CFD Python:求解Navier-Stokes方程的12個步驟(7) CFD Python:求解Navier-Stokes方程的12個步驟(8) CFD Python:求解Navier-Stokes方程的12個步驟(9) CFD Python:求解Navier-Stokes方程的12個步驟(10) CFD Python:求解Navier-Stokes方程的12個步驟(11) CFD Python:求解Navier-Stokes方程的12個步驟(12)
這個模組的最後兩個步驟會以不同的邊界條件求解二維Navier-Stokes方程。對於速度場 \vec{v},其向量形式的動量方程式為:
\frac{\partial \vec{v}}{\partial t}+(\vec{v}\cdot\nabla)\vec{v} = -\frac{1}{\rho}\nabla p + \nu \nabla^2\vec{v}
這表示三個純量方程式,分別對應三個速度分量 (u,v,w)。由於我們求解的是二維問題,因此只有兩個純量方程式。
還記得連續方程式嗎?這就是壓力的Poisson方程式用處!
步驟11:腔流問題(Cavity Flow)
下方是偏微分方程組:兩個速度分量 u、v 的方程式和一個壓力方程式:
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu \left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)
\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial y}+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right)
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2} = -\rho\left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right)
從之前的步驟已經知道如何離散所有的項。只有最後一個方程式有點陌生。但稍加耐心,它也不難!
離散方程式
首先離散化 u動量方程,如下所示:
\frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i,j-1}^{n}}{\Delta y} = -\frac{1}{\rho}\frac{p_{i+1,j}^{n}-p_{i-1,j}^{n}}{2\Delta x}+\nu\left(\frac{u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}}{\Delta x^2}+\frac{u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}}{\Delta y^2}\right)
同樣地,對於 v動量方程,可以進行如下離散:
\frac{v_{i,j}^{n+1}-v_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i,j-1}^{n}}{\Delta y} = -\frac{1}{\rho}\frac{p_{i,j+1}^{n}-p_{i,j-1}^{n}}{2\Delta y}+\nu\left(\frac{v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}}{\Delta x^2}+\frac{v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}}{\Delta y^2}\right)
最後,離散的壓力Poisson方程可以寫成下列形式:
\frac{p_{i+1,j}^{n}-2p_{i,j}^{n}+p_{i-1,j}^{n}}{\Delta x^2}+\frac{p_{i,j+1}^{n}-2p_{i,j}^{n}+p_{i,j-1}^{n}}{\Delta y^2} = \rho \left[ \frac{1}{\Delta t}\left(\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}+\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right) -\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x} - 2\frac{u_{i,j+1}-u_{i,j-1}}{2\Delta y}\frac{v_{i+1,j}-v_{i-1,j}}{2\Delta x} - \frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right]
你應該在筆記寫下這些方程式,並在書寫時默想每個項目。
與之前一樣,以迭代所需的方式重新排列方程式。首先是下個時間步長中的速度動量方程。
在 u 方向上的動量方程:
u_{i,j}^{n+1} = u_{i,j}^{n} - u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(u_{i,j}^{n}-u_{i-1,j}^{n}\right) - v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(u_{i,j}^{n}-u_{i,j-1}^{n}\right) - \frac{\Delta t}{\rho 2\Delta x} \left(p_{i+1,j}^{n}-p_{i-1,j}^{n}\right) + \nu \left(\frac{\Delta t}{\Delta x^2} \left(u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2} \left(u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}\right)\right)
在 v 方向上的動量方程:
v_{i,j}^{n+1} = v_{i,j}^{n} - u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(v_{i,j}^{n}-v_{i-1,j}^{n}\right) - v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(v_{i,j}^{n}-v_{i,j-1}^{n})\right) - \frac{\Delta t}{\rho 2\Delta y} \left(p_{i,j+1}^{n}-p_{i,j-1}^{n}\right) + \nu \left(\frac{\Delta t}{\Delta x^2} \left(v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2} \left(v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}\right)\right)
快完成了!現在來重新排列壓力Poisson方程:
p_{i,j}^{n} = \frac{\left(p_{i+1,j}^{n}+p_{i-1,j}^{n}\right) \Delta y^2 + \left(p_{i,j+1}^{n}+p_{i,j-1}^{n}\right) \Delta x^2}{2\left(\Delta x^2+\Delta y^2\right)} -\frac{\rho\Delta x^2\Delta y^2}{2\left(\Delta x^2+\Delta y^2\right)} \times \left[\frac{1}{\Delta t}\left(\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}+\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right)-\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x} -2\frac{u_{i,j+1}-u_{i,j-1}}{2\Delta y}\frac{v_{i+1,j}-v_{i-1,j}}{2\Delta x}-\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right]
初始條件為每處的 u、v、p 等於 0,而邊界條件為:
u = 1 在 y = 2 (頂蓋)
其他邊界上的u, v = 0
\frac{\partial p}{\partial y}=0在 y = 0
p = 0 在 y = 2
\frac{\partial p}{\partial x}=0在 x = 0, 2
腔流問題實作
import numpy
from matplotlib import pyplot, cm
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inlinenx = 41
ny = 41
nt = 500
nit = 50
c = 1
dx = 2 / (nx - 1)
dy = 2 / (ny - 1)
x = numpy.linspace(0, 2, nx)
y = numpy.linspace(0, 2, ny)
X, Y = numpy.meshgrid(x, y)
rho = 1
nu = .1
dt = .001
u = numpy.zeros((ny, nx))
v = numpy.zeros((ny, nx))
p = numpy.zeros((ny, nx))
b = numpy.zeros((ny, nx))上面的壓力Poisson方程很容易在書寫時出錯。下方 build_up_b 函式代表方括號內容,使整個壓力Poisson方程容易處理一些。
def build_up_b(b, rho, dt, u, v, dx, dy):
b[1:-1, 1:-1] = (rho * (1 / dt *
((u[1:-1, 2:] - u[1:-1, 0:-2]) /
(2 * dx) + (v[2:, 1:-1] - v[0:-2, 1:-1]) / (2 * dy)) -
((u[1:-1, 2:] - u[1:-1, 0:-2]) / (2 * dx))**2 -
2 * ((u[2:, 1:-1] - u[0:-2, 1:-1]) / (2 * dy) *
(v[1:-1, 2:] - v[1:-1, 0:-2]) / (2 * dx))-
((v[2:, 1:-1] - v[0:-2, 1:-1]) / (2 * dy))**2))
return b定義 pressure_poisson 函式,以幫助區分不同回合的計算。請注意偽時間變量 nit 的存在。Poisson計算中的子迭代有助於確保一個無發散場(divergence-free field)。
def pressure_poisson(p, dx, dy, b):
pn = numpy.empty_like(p)
pn = p.copy()
for q in range(nit):
pn = p.copy()
p[1:-1, 1:-1] = (((pn[1:-1, 2:] + pn[1:-1, 0:-2]) * dy**2 +
(pn[2:, 1:-1] + pn[0:-2, 1:-1]) * dx**2) /
(2 * (dx**2 + dy**2)) -
dx**2 * dy**2 / (2 * (dx**2 + dy**2)) *
b[1:-1,1:-1])
p[:, -1] = p[:, -2] # dp/dx = 0 at x = 2
p[0, :] = p[1, :] # dp/dy = 0 at y = 0
p[:, 0] = p[:, 1] # dp/dx = 0 at x = 0
p[-1, :] = 0 # p = 0 at y = 2
return p最後,腔流方程的其餘部分包在 cavity_flow 函式內部,使我們能輕鬆繪製腔流求解器在不同時間長度下的結果。
def cavity_flow(nt, u, v, dt, dx, dy, p, rho, nu):
un = numpy.empty_like(u)
vn = numpy.empty_like(v)
b = numpy.zeros((ny, nx))
for n in range(nt):
un = u.copy()
vn = v.copy()
b = build_up_b(b, rho, dt, u, v, dx, dy)
p = pressure_poisson(p, dx, dy, b)
u[1:-1, 1:-1] = (un[1:-1, 1:-1]-
un[1:-1, 1:-1] * dt / dx *
(un[1:-1, 1:-1] - un[1:-1, 0:-2]) -
vn[1:-1, 1:-1] * dt / dy *
(un[1:-1, 1:-1] - un[0:-2, 1:-1]) -
dt / (2 * rho * dx) * (p[1:-1, 2:] - p[1:-1, 0:-2]) +
nu * (dt / dx**2 *
(un[1:-1, 2:] - 2 * un[1:-1, 1:-1] + un[1:-1, 0:-2]) +
dt / dy**2 *
(un[2:, 1:-1] - 2 * un[1:-1, 1:-1] + un[0:-2, 1:-1])))
v[1:-1,1:-1] = (vn[1:-1, 1:-1] -
un[1:-1, 1:-1] * dt / dx *
(vn[1:-1, 1:-1] - vn[1:-1, 0:-2]) -
vn[1:-1, 1:-1] * dt / dy *
(vn[1:-1, 1:-1] - vn[0:-2, 1:-1]) -
dt / (2 * rho * dy) * (p[2:, 1:-1] - p[0:-2, 1:-1]) +
nu * (dt / dx**2 *
(vn[1:-1, 2:] - 2 * vn[1:-1, 1:-1] + vn[1:-1, 0:-2]) +
dt / dy**2 *
(vn[2:, 1:-1] - 2 * vn[1:-1, 1:-1] + vn[0:-2, 1:-1])))
u[0, :] = 0
u[:, 0] = 0
u[:, -1] = 0
u[-1, :] = 1 # set velocity on cavity lid equal to 1
v[0, :] = 0
v[-1, :] = 0
v[:, 0] = 0
v[:, -1] = 0
return u, v, p從 nt = 100 開始,看看求解結果:
u = numpy.zeros((ny, nx))
v = numpy.zeros((ny, nx))
p = numpy.zeros((ny, nx))
b = numpy.zeros((ny, nx))
nt = 100
u, v, p = cavity_flow(nt, u, v, dt, dx, dy, p, rho, nu)fig = pyplot.figure(figsize=(11,7), dpi=100)
# plotting the pressure field as a contour
pyplot.contourf(X, Y, p, alpha=0.5, cmap=cm.viridis)
pyplot.colorbar()
# plotting the pressure field outlines
pyplot.contour(X, Y, p, cmap=cm.viridis)
# plotting velocity field
pyplot.quiver(X[::2, ::2], Y[::2, ::2], u[::2, ::2], v[::2, ::2])
pyplot.xlabel('X')
pyplot.ylabel('Y');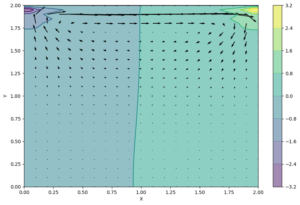
您可以看到正在形成兩個不同的壓力區域,以及頂蓋驅動腔流的螺旋流場。嘗試不同的 nt 值,看看系統需要多長時間才能穩定。
u = numpy.zeros((ny, nx))
v = numpy.zeros((ny, nx))
p = numpy.zeros((ny, nx))
b = numpy.zeros((ny, nx))
nt = 700
u, v, p = cavity_flow(nt, u, v, dt, dx, dy, p, rho, nu)u = numpy.zeros((ny, nx))
v = numpy.zeros((ny, nx))
p = numpy.zeros((ny, nx))
b = numpy.zeros((ny, nx))
nt = 700
u, v, p = cavity_flow(nt, u, v, dt, dx, dy, p, rho, nu)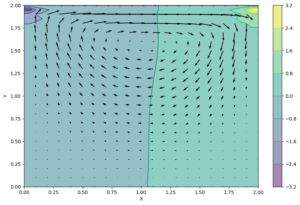
quiver圖顯示了網格格點處的速度大小。(實際上,我們只顯示了一半的點,否則會有點混亂。上面的X[::2,::2]是一種方便的語法,要求每隔一個點來顯示)。另一種可視化腔內流動的方法是使用流線圖(streamplot):
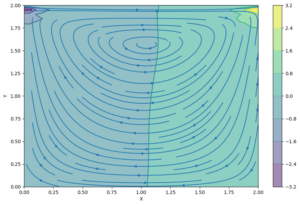
參考資料

本著作係採用創用 CC 姓名標示 4.0 國際 授權條款授權.
