(本文經Prof. Lorena A. Barba授權轉載翻譯自Prof. Lorena A. Barba的教材”12 Steps to Navier-Stokes”,原文鏈結請參照底下參考資料)
Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved BSD-3 license. (c) Lorena A. Barba, Gilbert F. Forsyth 2017. Thanks to NSF for support via CAREER award #1149784.
CFD Python:求解Navier-Stokes方程的12個步驟(1) CFD Python:求解Navier-Stokes方程的12個步驟(2) CFD Python:求解Navier-Stokes方程的12個步驟(3) CFD Python:求解Navier-Stokes方程的12個步驟(4) CFD Python:求解Navier-Stokes方程的12個步驟(5) CFD Python:求解Navier-Stokes方程的12個步驟(6) CFD Python:求解Navier-Stokes方程的12個步驟(7) CFD Python:求解Navier-Stokes方程的12個步驟(8) CFD Python:求解Navier-Stokes方程的12個步驟(9) CFD Python:求解Navier-Stokes方程的12個步驟(10) CFD Python:求解Navier-Stokes方程的12個步驟(11) CFD Python:求解Navier-Stokes方程的12個步驟(12)
步驟3:一維擴散方程式
一維擴散方程式可寫成如下形式:
\frac{\partial u}{\partial t}= \nu \frac{\partial^2 u}{\partial x^2}
你要注意的是這並不像前兩個步驟的方程式那麼簡單,這個方程式包含二次微分項。要先來學習如何處理它!
離散\frac{\partial ^2 u}{\partial x^2}
二次微分項在幾何上可以表示成第一微分項給定的曲線切線。可以透過中央差分來離散二次微分項:結合一次微分項的前向差分與後向差分。考量u_i附近的u_{i+1}與u_{i-1}及其泰勒展開式:
u_{i+1} = u_i + \Delta x \frac{\partial u}{\partial x}\bigg|_i + \frac{\Delta x^2}{2} \frac{\partial ^2 u}{\partial x^2}\bigg|_i + \frac{\Delta x^3}{3!} \frac{\partial ^3 u}{\partial x^3}\bigg|_i + O(\Delta x^4)u_{i-1} = u_i - \Delta x \frac{\partial u}{\partial x}\bigg|_i + \frac{\Delta x^2}{2} \frac{\partial ^2 u}{\partial x^2}\bigg|_i - \frac{\Delta x^3}{3!} \frac{\partial ^3 u}{\partial x^3}\bigg|_i + O(\Delta x^4)
如果將這兩個展開式相加,你可以發現奇數微分項將會互相抵銷。此外,如果忽略任何O(\Delta x^4)展開項與其餘更高次方項(實際上這些次方項數值也很小),那我們便能將兩個展開式的加總寫成用來求解二次微分項的形式。
u_{i+1} + u_{i-1} = 2u_i+\Delta x^2 \frac{\partial ^2 u}{\partial x^2}\bigg|_i + O(\Delta x^4)接著再調整一下式子,二次微分項可表示成:
\frac{\partial ^2 u}{\partial x^2}=\frac{u_{i+1}-2u_{i}+u_{i-1}}{\Delta x^2} + O(\Delta x^2)
回到步驟3
現在可以將離散後的一維擴散方程式寫成下列形式:
\frac{u_{i}^{n+1}-u_{i}^{n}}{\Delta t}=\nu\frac{u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n}}{\Delta x^2}
如同前兩個步驟,一旦有了初始條件,剩下的未知項就只有u_{i}^{n+1}。因此,為了求解未知項,重新調整方程式如下:
u_{i}^{n+1}=u_{i}^{n}+\frac{\nu\Delta t}{\Delta x^2}(u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n})
到這裡,已經能撰寫一個隨著時間推進來求解上述方程的程式,但我們仍然需要初始條件,因此沿用帽函式(hat function),在t = 0的時候,0.5\le x\le 1這個區間內u = 2,其餘各處 u = 1。現在我們已經做好數值計算的準備了!
import numpy #loading our favorite library
from matplotlib import pyplot #and the useful plotting library
%matplotlib inline
nx = 41
dx = 2 / (nx - 1)
nt = 20 #the number of timesteps we want to calculate
nu = 0.3 #the value of viscosity
sigma = .2 #sigma is a parameter, we'll learn more about it later
dt = sigma * dx**2 / nu #dt is defined using sigma ... more later!
u = numpy.ones(nx) #a numpy array with nx elements all equal to 1.
u[int(.5 / dx):int(1 / dx + 1)] = 2 #setting u = 2 between 0.5 and 1 as per our I.C.s
un = numpy.ones(nx) #our placeholder array, un, to advance the solution in time
for n in range(nt): #iterate through time
un = u.copy() ##copy the existing values of u into un for i in range(1, nx - 1):
u[i] = un[i] + nu * dt / dx**2 * (un[i+1] - 2 * un[i] + un[i-1])
pyplot.plot(numpy.linspace(0, 2, nx), u);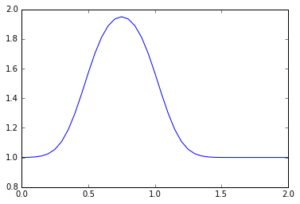
參考資料
- 12 steps to Navier–Stokes: Step 3: Diffusion Equation in 1-D,Lorena A. Barba

本著作係採用創用 CC 姓名標示 4.0 國際 授權條款授權.
