淺談CFD學習之路

CAE專欄的第一篇文章就先來聊聊我對CFD學習的看法吧！CFD是Computational Fluid Dynamics的縮寫，中文名稱為計算流體力學。顧名思義就是運用電腦來求解流體力學的問題，對CFD有點概念的人都應該知道流體統御方程式為偏微分方程，目前大多數偏微分方程尚未有解析解，因此才以數值方法來求解流體問題。

本文預設給已對CFD有些概念的讀者看，非相關領域者有些疑惑是正常的喔！在後續系列文章中，主廚也會更為全面地介紹CFD這個主題。

今天主要聊的是我個人學習CFD的想法。當然，每個人適合的學習方法不同，能夠以這個為基礎調整，或者是找出適合自己的學習心法。

釐清CFD學習方向

從計算流體力學的名稱可知CFD包含兩個部分，分別是數值方法與流體力學。這兩大類又可以再往下細分，好比說數值方法中包含離散方式與求解演算法等等，流體力學則是講述流體的基本現象與力學概念，如果還有其他考量，比如燃燒、化學反應等等，涉及的學科就會更加廣泛。綜上所述，學習計算流體力學就是學習這些數值方法以及求解對象。

首先，初入CFD的新手要先釐清自己的學習取向究竟是CFD本身還是應用CFD來解決流體問題。如果是研究CFD本身，那你學習數值方法的比重自然要提高；反過來說，若你本身是應用CFD解決特定流體問題，數值方法的比重也許會較前者來的低一些，但這不代表學習數值方法不重要，若是不懂你用的工具，沒辦法針對不同問題套用合適數值方法，最後結果很可能是Garbage in, garbage out。

打個比方而言，如果要求解流場中不同尺度的渦流，LES模型會比RANS模型來的更適合一些。又或者是採用一階迎風差分格式(First-order upwind scheme)雖然求解較為穩定，但會有假擴散(False diffusion)的問題。無論學習取向是CFD本身或是應用CFD來解決問題，數值方法與相關流體知識都是缺一不可，但學習取向的不同會影響到學習比重的分配。

CFD數值方法的學習

前面提到不管是什麼學習方向，學習數值方法都是必要的。以目前商業主流而言，求解流體問題一般都是用有限體積法(Finite volume method)，以主廚讀過的CFD書籍來看，這些書本的編排方式大致如下：

1. 數學理論回顧：不同種類的PDE特性、向量微積分、矩陣操作等等
2. 統御方程式(Governing equations)介紹：流體力學簡介與相關統御方程式推導
3. 離散格式介紹：網格劃分、方程式離散格式與性質探討
4. 求解演算法介紹：常運用於數值流力求解的演算法介紹，如SIMPLE、PISO等等。

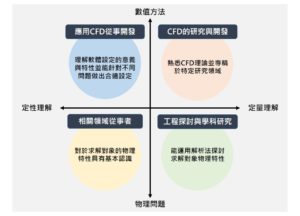
除此之外，書本中也會提到邊界條件、紊流模型或者是源項(Source term)的處理等等。從上面歸納來看，我們不難發現CFD的學習與數學脫不了關係，如果想成為CFD的專家，這些學習也是你我都得面對的。話雖如此，我們依然可以選擇定性學習或是定量學習。

看到這兒，您可能會有些疑惑，定性學習與定量學習的差異是什麼呢？

數值方法的定性學習

所謂的定性學習就是對數值方法有定性上的了解，好比說用來判斷網格品質的aspect ratio、skewness分別代表什麼；又或者是紊流模型k-ε、SST的差異與使用時機等等。對於使用CFD商業軟體的學習者來說，也許不用熟悉背後數學理論，但要能選擇適當模型或算法來求解問題，才能確保模擬結果準確並更快達到收斂。

數值方法的定量學習

至於定量學習是對數值方法有定量上的理解，熟悉離散格式與演算法的數學算法與邏輯，或是不同物理模型背後的方程式，這部分就像是武功內力一樣，當你從定性理解來到定量理解的階段後，能夠清楚知道軟體上每個操作對數學式子的影響，看待CFD也會有不同的感受。

CFD模擬對象的學習

數值方法在CFD裡面扮演著求解工具的角色，既然是求解工具，勢必會有求解對象的存在。

試想一下，如果今天要求解包含電化學反應的流體問題，卻對電化學一竅不通，這樣還能做出合理的假設與邊界條件設定嗎？所以運用CFD解決問題時，必須對求解對象有一定程度了解。同樣地，這部分也分為定性理解與定量理解。

模擬對象的定性學習

對於模擬對象的定性理解關係到怎麼設定模擬目標、邊界條件的處理、物理模型的選用等等。打個比方來說，如果今天求解旋轉機械的問題，那你可能要知道風扇的性能評估指標，不同風扇具有怎樣不同的特性，套用什麼物理模型才能求解旋轉機械。簡而言之，對這個流體機械有定性上的了解，才能合理設置完整的模擬流程。

模擬對象的定量學習

而模擬對象定量理解又分成數值解與解析解，數值解的部分主要是理解每個物理模型或邊界條件對應的數學式，相較於數值解，解析解多半更容易查看變數間的關係，便於事前評估或事後驗證，建立工程上的直覺。

CFD學習資源分享

前面主要是幫大家釐清學習取向，不過會進來看這篇文章的你肯定也想知道有哪些學習資源可以參考，因此主廚幫大家歸納幾個不同面向的CFD學習資源，希望能給各位CFDer一些參考。

1. Computational Fluid Dynamics, John D. Anderson：基於有限差分法來介紹CFD理論，適合初學者
2. The Finite Volume Method in Computational Fluid Dynamics – An Advanced Introduction with OpenFOAM and Matlab：基於有限體積法來介紹CFD理論，書內有OpenFOAM部分程式碼解說
3. CFD NINJA ：ANSYS教學頻道，手把手教你模擬設定
4. Ansys How To Videos：ANSYS教學頻道，手把手教你模擬設定
5. CFD Python: 12 steps to Navier-Stokes：Prof. Barba的教學網頁，透過12道Python數值算例，最後帶你實現Cavity flow與Channel flow等經典算例求解
6. Finite Difference Computing with PDEs: A Modern Software Approach：基於有限差分法來介紹數值方法並用Python實現書內數值方法，適合對數值分析程式有興趣的讀者
7. 各家商業軟體的Manual：原廠訓練資料或manual是個不錯的參考資料，但需要一些CFD理論基礎
8. 數值分析開放式課程：國內的話有台大黃美嬌教授與政大曾正男教授的課程，適合習慣以授課方式來學習的對象
9. CFD Online Discussion Forums：討論CFD的論壇，內有各種疑難雜症的討論

CFD學習歷程分享

由於有讀者詢問主廚學習CFD的心路歷程與方法，因此2022/2/12於《淺談CFD學習之路》本文新增此段落，希望個人經驗分享能夠達到拋磚引玉的效果。

主廚最早是從商業軟體開始接觸CFD，除了看網路教材以外，也有買些介紹CFD軟體的書來看，初學者階段主要是熟悉軟體操作與設定，雖然對部分設定與邊界條件有些概念，但對求解算法一竅不通，這時只求模擬收斂。

而為了讓模擬順利收斂，也會嘗試不同設定對求解的影響或是到CFD Online Discussion Forum看看各路大神的想法，試著歸納每個設定與算法的意義與特性。這個階段主要是定性上的學習並應用CFD了解流體現象。

隨著經手案例增加，模擬準確性也漸漸受到考驗，也有很大一部分是我對模擬結果沒有把握，這時才開始主動學習CFD理論，學習途徑不外乎就是修課或讀書，雖然在定性學習的階段也會被動接收CFD理論，但通常只是看個感覺而已。一段時間的累積後，對於CFD理論也有基本理解，這個階段主要是定量上的學習，對於模擬設定有更深刻的認知，也比較能從數學上的角度來理解模擬設定。

再來就是商業軟體漸漸無法滿足研究或是開發上的需求，除了再次加強CFD基礎以外，也開始寫些程式來求解特定問題。這個階段同樣是定量學習，但會更深入求解過程的實踐與細節，釐清自己思考上的盲點，對於算法有更深刻的認知。

雖然每個過程都只用了幾句話帶過，但從起初只求模擬收斂到後來發展數值分析程式求解特定問題，每個階段都花費不少時間，而從定性到定量的過渡期更是需要耐心，有一位好老師或一本好書固然重要，但主廚認為學習心態才是根本，面對過渡期的心態有底下幾個重點：

從定性到定量需要大量思考

定性描述可以幫助我們快速理解不同方法的特性，不太需要深入思考就能吸收這些結果。但CFD定量上的學習伴隨大量數學，要理解這些數學表達與計算邏輯，需要耐心思考與反芻，所以請做好這方面的心理準備！

從定性到定量需要多方學習

在思考與反芻的過程中，通常都會遇到學習上的盲點，無論怎麼讀就是讀不通，如果身邊有人可以請教，不妨試著討論看看。如果沒有這樣的對象，可以從不同資料來理解同一個學習對象。比如說這本書的方程式推導不管看了幾次都無法理解，也許原先那本書在推導過程省略的觀念恰巧是你卡關的盲點，這時可以看看其他書本如何推導，補上不足的那塊拼圖。

從定性到定量需要循序漸進

CFD是一門綜合學科，除了流體力學以外，也涉及到偏微分方程與線性代數等學科，複雜難懂的數學令人退避三舍，但這些複雜的數學表達也是由基本觀念建立起來，這也是為什麼教科書開頭會有個介紹CFD常用數學的章節。

所以學習CFD的心態必須要循序漸進，如果一開始就想處理複雜的流體計算問題，還沒做之前就先放棄一半了。所以哪怕是跟流體毫無關聯也沒關係，先從簡單的數值分析案例開始，至少執行過程中遇到問題比較有頭緒，而基本的數值分析觀念對於後續學習其他學科或是計算流體力學會更有幫助。

目標/需求導向的學習模式

最後一點則是目標導向的學習模式，有個目標或需求會讓你的學習方向更加明確，更容易判斷學習項目的必要性與先後順序。以修課這件事情來講，在沒有目標的情況下可能聽起來有懂就好，但如果目標是寫個簡單的求解器，你就會判斷這些內容需不需要深入理解，如果需要的話，那我要如何把這些內容拿來實踐求解器的哪個部分，你的目標會決定你的思考深度。

而當目標涵蓋範圍太廣的時候，需要將一個目標切成好幾個小目標，循序漸進完成各個小目標，也就是前面第三點說的。沒辦法一次到位就分成好幾次，沒有硬功夫就下功夫鑽研，累積久了自然就有功夫。

主廚結語

主廚下了個淺談CFD學習之路的標題，是因為CFD有著太多需要學習的東西。若您從事學術研究或前端開發的話，可能會遇到商業軟體無法滿足需求或是研究上需要驗證數值算法的狀況，這時需要對CFD有更深入的定量了解，才能撰寫程式來解決更深入的難題。若您在業界從事CFD模擬的話，如何處理複雜的幾何模型，快速得到模擬結果，也許才是您當下模擬的重點。

CFD的學習是條漫漫長路，主廚自己也還在學習路上，這些經驗與看法不見得完全適用在你身上，但希望一點經驗分享能夠幫助到同樣學習CFD的你。