由於多數偏微分方程無法求得解析解,為了解決這個問題,學者們發展出不同的數值方法來求得偏微分方程的近似解,其中一種方法稱為有限體積法(Finite Volume Method)。
透過有限體積法,我們能將偏微分方程轉換成線性代數方程式並使用電腦求解,而將偏微分方程轉換為線性代數方程式的步驟稱為離散,今天就來與各位聊聊有限體積法離散原理!
《延伸閱讀:CFD離散程序簡介,3個不可不知的離散步驟!》
傳輸方程有限體積法離散
STEP1:運用散度定理將傳輸方程積分式轉換為環積分
為了解釋有限體積法的離散概念,我們以二維傳輸方程作為例子來介紹,而傳輸方程如下:
\frac{\partial (\rho \phi)}{\partial t} + \triangledown \cdot(\rho \mathbf{v} \phi) = \triangledown \cdot (\Gamma \triangledown\phi) + Q - (1)
其中ø為純量變數,t為時間,ρ為密度,v為速度向量,Γ為擴散係數,Q為源項。若上述傳輸方程式處於穩態,意即不考慮時間項變化,可將方程式改寫成式(2)。
\triangledown \cdot(\rho \mathbf{v} \phi) = \triangledown \cdot (\Gamma \triangledown\phi) + Q - (2)
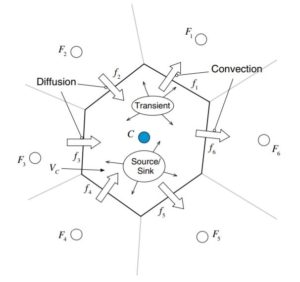
在圖1中的元素C區域內將式(2)積分,即可得到式(3)。接著透過散度定理(Divergence theorem)將式(3)對流項與擴散項的體積分轉換為環積分,即可得式(4)。
\int_{V_C}\triangledown \cdot(\rho \mathbf{v} \phi) dV= \int_{V_C}\triangledown \cdot (\Gamma \triangledown\phi) dV+ \int_{V_C}Q dV- (3)
\oint_{\partial Vc}(\rho \mathbf{v} \phi)dS = \oint_{\partial Vc} (\Gamma \triangledown\phi)dS + \int_{V_C}QdV - (4)
STEP2:控制容積的面通量總和
我們將傳輸方程中的擴散項與對流項轉換成環積分形式,環積分代表擴散項通量與對流項通量沿著封閉曲線積分。對於元素C而言,即是將各個面上的通量相加,因此可將擴散項與對流項環積分以式(5) – 式(8)表示。
J^{\phi,c} = \rho \mathbf{v}\phi - (5)
J^{\phi,D} = - \Gamma \triangledown \phi - (6)
\oint_{{\partial V_c}}J^{\phi,c} \cdot dS = {\sum\limits_{faces(V_c)}} \left ( \int_{f} (\rho \mathbf{v}\phi) \cdot dS\right ) - (7)
\oint_{{\partial V_c}}J^{\phi,D} \cdot dS = {\sum\limits_{faces(V_c)}} \left ( \int_{f} (\Gamma \triangledown \phi) \cdot dS\right ) - (8)
其中J^{\phi,c}為對流項通量,J^{\phi,D}為擴散項通量。
儘管式(7)與式(8)將環積分轉換成元素C各個面上的通量積分總和,卻依然有著積分項,對於電腦而言並不是個方便計算的形式,因此我們需要進一步離散積分項,導入高斯積分點的概念,將面通量的積分項簡化並以式(9)來表示。
\int_{f} J^{\phi} \cdot d\textbf{S} = \int_{f} (J^{\phi} \cdot \textbf{n}) dS = \sum\limits_{ip(f)}(J^{\phi} \cdot \textbf{n})_{ip} \omega_{ip} S_f - (9)
其中ip指的是積分點(integration point),而ip(f)為積分點數量,\omega_{ip}則是權重函數。若取表面中心點作為高斯積分點,則\omega_{ip}等於1。基於式(9)的概念,可以將式(7)與式(8)表示成式(11)與式(12),即控制容積的面通量總和。
\oint_{{\partial V_c}} \left ( \int_{f} (\rho \mathbf{v}\phi) \cdot dS\right )= {\sum\limits_{faces(V_c)}}\sum\limits_{ip(f)}(\rho \mathbf{v}\phi)_{ip} \omega_{ip} \textbf{S}_f - (11)
\oint_{{\partial V_c}} \left ( \int_{f}(-\Gamma \triangledown \phi) \cdot dS\right )= {\sum\limits_{faces(V_c)}}\sum\limits_{ip(f)}(-\Gamma \triangledown \phi)_{ip} \omega_{ip} \textbf{S}_f - (12)
STEP3:控制容積總通量線性化
求得控制容積的面通量總和之後,對於圖2的元素C而言,在不考慮源項且表面中心作為高斯積分點的情形下,半離散穩態方程式可被簡化成下列形式,如式(13)所示。
\sum\limits_{f-nb(C)}(\rho \textbf{v}\phi - \Gamma^{\phi }\triangledown \phi) \cdot \textbf{S}_f = 0- (13)

由於一般物理量的變數都是儲存於各個元素中心,如圖2中的點C、點F1至點F6。因此,需要將式(13)的面通量以元素中心變數表示,此步驟稱為通量線性化(Flux linearlization)。若元素C中心點物理量為 \phi_C且周遭元素中心點物理量為 \phi_F,則線性化後的式子可表示成式(14)的形式。
\textbf{J}_f \cdot \textbf{S}_f = FluxC_f \ \phi_C + FluxF_f \ \phi_F + FluxVf- (14)
其中FluxCf與FluxFf分別為元素C中心點與周遭元素中心點線性化後的係數項,FluxVf為非線性化項。要特別注意的是,式(14)為線性化後的通式,無論是哪種離散項與離散格式,最終都能被表示成式(14)的形式。若將總通量以各面通量總和的形式來表達,式(14)可改寫成式(15)。
\sum\limits_{f-nb(C)}(\textbf{J}_f \cdot \textbf{S}_f) = \sum\limits_{f-nb(C)}(FluxC_f \ \phi_C + FluxF_f \ \phi_F + FluxVf)- (15)
我們進一步將式(15)化簡並以更精簡的符號表示,結果如式(16) – 式(19)所示。至此完成以元素中心變數來表示離散式的通式。
a_C \phi_C + \sum\limits_{f-nb(c)}(a_F \phi F) = b_C- (16)
a_C = \sum\limits_{f-nb(c)}FluxCf- (17)
a_F = FluxFf- (18)
b_C = -\sum\limits_{f-nb(c)}FluxVf- (19)
主廚結語
本次與各位介紹穩態傳輸方程式的離散化,其基本概念為將偏微方程轉換為積分式後,運用散度定理將積分式轉換成環積分,由於環積分為沿著封閉曲線的積分,對控制容積而言,即為各表面的積分項總和。
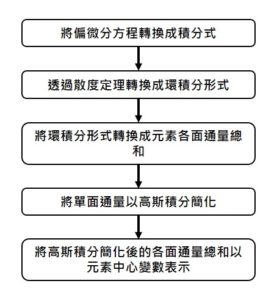
有了各表面的通量積分項總和後,對於單一表面的通量積分而言,可利用高斯積分點將其轉換成線性代數方程式,便能求得各表面通量總和的線性代數方程。然而,由於各變數儲存於元素中心點,需要進一步將各表面的通量總和以元素中心變數來表示,整個離散流程如圖3所示。
對於初次接觸有限體積法的人而言想必有些難懂,但只要釐清每個步驟背後的意義,其實並沒有想像中困難。如果對這類文章有興趣的話,可以按讚科技雞湯Facebook,持續追蹤最新消息喔!