什麼是公差分析?
在《什麼是公差?公差標註基本介紹!》這篇文章中提到公差指的是特定尺寸的容許誤差範圍,而一項產品中包含許多零件,每個零件又包含許多尺寸,如果不妥善決定公差,產品便難以組裝,也會影響功能與成本等等。
因此,今天要來與各位介紹公差分析。而公差分析指的是一種用來審視零件尺寸公差分配是否合理的方法,透過封閉尺寸鏈的公差增減關係來判斷是否需要調整公差,進而在產品功能與成本間取得平衡,滿足設計需求。
什麼是尺寸鏈?
那在聊聊公差分析之前,要先各位介紹尺寸鏈的概念,那什麼是尺寸鏈呢?尺寸鏈指的即是在產品裝配關係中,頭尾相接的封閉尺寸組合,我們來看看下方例子。
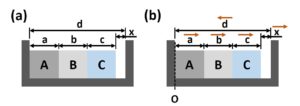
A、B、C三個零件放在凹槽中,寬度分別為a、b、c,而凹槽寬度為d,三個零件對位後與凹槽間的間隙為x,如圖2(a)所示。在這個裝配關係中,a、b、c、x、d幾個尺寸頭尾相接所形成的環狀尺寸組合即為尺寸鏈。
若以O為原點,往右為正的話,可將a、b、c、x的方向定義為正,尺寸d的方向為負,並列出下列關係式,從關係式可知一個封閉尺寸鏈為了滿足封閉性,正負方向上的尺寸相加後為0。
a + b + c + x - d = 0
公差分析計算
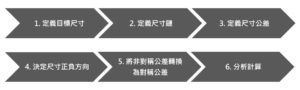
定義目標尺寸
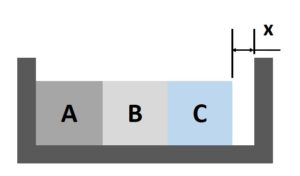
了解尺寸鏈的概念後,我們來看看公差分析的例子。假設A、B、C三個方塊要能順利放進凹槽中,餘隙量X需大於0,才能避免干涉,為了確認現有尺寸公差是否會影響組裝,我們將目標尺寸定義為X,如圖3所示。
定義尺寸鏈
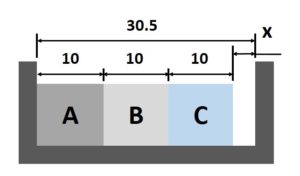
決定目標尺寸之後,下一步就是找出目標尺寸的關聯尺寸,從組裝關係可知餘隙量分別與三個零件寬度與凹槽寬度相關,便能決定與目標尺寸相關的封閉尺寸鏈,如圖4所示。
定義尺寸公差
前面提及任何零件尺寸必然存在誤差,為了確保誤差在容許範圍內,會設定公差來規範尺寸誤差範圍。而公差的設定需要考量很多因素,像是材質、加工程序、功能性等等。假設我們已經根據經驗提出一組看似可行的公差,如圖5所示,接著就要透過公差分析來判斷這組公差是否能滿足裝配關係。
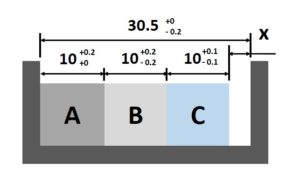
決定尺寸正負方向
一個完整的尺寸鏈為了滿足封閉性,正負方向的尺寸相加後必然等於0。假設我們以O點為原點,為了再次回到原點,順著尺寸鏈定義每個尺寸的方向,便能決定三個方塊尺寸與餘隙量為正向,而凹槽寬度為負向。
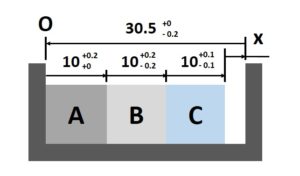
將非對稱公差轉換為對稱公差
再來為了確保等等計算上的公差變動關係一致,需要將非對稱公差轉換為對稱公差,而對稱公差具有單一尺寸正負公差數值相同的特性。因此,對此案例而言,僅有零件A寬度與凹槽寬度為非對稱公差。
以零件A寬度的例子來看,該尺寸公稱值為10,上下公差分別為0與0.2,代表該尺寸最小為10,最大為10.2。為了滿足尺寸變動範圍與對稱公差的要求,將公稱值從10改為10.1,上下公差分別為-0.1與0.1,如此便能在對稱公差的情形下,滿足該尺寸最小為10,最大為10.2的變動範圍,如圖7。
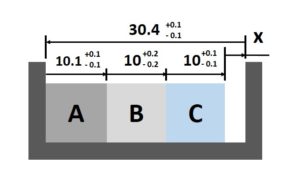
分析計算 – 極值法(Worst Case)
公差分析分別有極值法與均方根法。無論是哪種方法,都要先算出餘隙量X的公稱值,再來考慮各零件公差對餘隙量的影響。公稱值的計算需考慮尺寸正負,計算如下:
D_x = D_D - D_A - D_B - D_C = 30.4 - 10.1 - 10 -10 = 0.3
得到X的公稱值後,接著計算X的單向公差,計算方式為各尺寸公差加總,如下:
T_x = T_A + T_B+ T_C+ T_D = 0.1 + 0.2 + 0.1 + 0.1 = 0.5
根據X的公稱值與公差範圍,可計算餘隙量X的最大值與最小值如下:
D_{X, min} = 0.3 - 0.5 = -0.2
D_{X, max} = 0.3 + 0.5 = 0.8
從計算結果可知餘隙量可能出現負值,代表零件與凹槽間的裝配可能會出現干涉,從極值法的觀點來看,這組公差設計並不能滿足裝配需求,因此需要調整零件公差來滿足裝配考量。
分析計算 – 均方根法(RSS)
極值法的計算考量各個公差的極值,這種計算方式雖然最為安全,但同時對公差要求也較為嚴苛。對於量產而言,零件尺寸多半是公差範圍內的常態分佈,零件尺寸落在極端值的機率不高。而均方根法即是根據這種機率分布的概念來計算。
均方根法同樣要先計算公稱值,其計算方法與極值法相同,故不再贅述。在公差計算上則是將各尺寸公差的平方加總開根號以取得目標尺寸的公差,式子如下:
T_x = \sqrt{\sum_{i=1}^{n}T_i^2}=\sqrt{0.1^2+0.2^2+0.1^2+0.1^2}=0.265
根據X的公稱值與公差範圍,可計算餘隙量X的最大值與最小值如下:
D_{X, min} = 0.3 - 0.265 = 0.035
D_{X, max} = 0.3 + 0.265 = 0.565
從均方根法的角度來看,此組公差設計能滿足裝配需求,無需特別更改。
主廚結語
此次與各位介紹公差分析的兩種方法,分別是極值法與均方根法。一般而言,極值法的計算方式對於公差要求較為嚴苛,均方根法則是考慮誤差常態分佈的因素,故能放緩公差要求,選用哪種計算方式則仰賴製造情況、零件個數等等因素。
