前陣子有人問主廚什麼是迎風格式(upwind scheme),於是藉此機會來寫一篇有關迎風格式的介紹。高手就不必說了,即使是CFD初學者也或多或少聽過迎風格式,不過你知道什麼是迎風格式嗎?迎風格式又是用在什麼地方呢?這次就來聊聊迎風格式吧!
什麼是離散格式?
談談迎風格式前,要先知道什麼是離散格式。由於流體統御方程式(Governing equations)為偏微分方程,且這類偏微分方程目前沒有理論解,因此需要將統御方程式轉換成線性代數方程來求解,這個轉換過程稱為離散化。
在先前的文章中,主廚曾經介紹有限體積法如何離散方程式,然而有限體積法只是一種建立數值模型的基本架構。離散格式則是在這個基本架構下用來離散方程式特定項的過程與方法,這次要介紹的迎風格式也是離散格式其中一種。
延伸閱讀1:《CFD離散程序簡介,3個不可不知的離散步驟!》
延伸閱讀2:《有限體積法離散原理:傳輸方程式》
什麼是迎風格式?
大致對離散格式有個概念後,我們直接用一個例子來看看什麼是迎風格式,底下用一個一維線性對流方程來說明迎風格式如何運作,其中c為常數。
\frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = 0
由於迎風格式是一種針對空間項的離散方法,因此我們只將迎風格式套用在空間項,當常數c大於0的時候,使用後向差分來離散空間項;反之,當常數c小於0的時候,使用前向差分來離散空間項,如下式所示。
\frac{u_i^{n+1}-u_i^n}{\Delta t} + c \frac{u_i^n - u_{i-1}^n}{\Delta x} = 0, c > 0
\frac{u_i^{n+1}-u_i^n}{\Delta t} + c \frac{u_{i+1}^n - u_{i}^n}{\Delta x} = 0, c < 0
這個就是迎風格式的運作方式,不過看到這兒你可能會一頭霧水,單看這個例子的話,雖然知道如何使用迎風格式來離散方程式,但為什麼得根據常數c的正負來分別使用前向差分或後向差分呢?有這個必要嗎?
答案是有的,底下我們就來看看迎風格式的特性!
迎風格式的特性是什麼?
聊聊迎風格式的特性之前,我們先來複習一下Navier-Stokes方程式,如下式,其中方程式左邊分別是時間項、對流項,右邊則分別是壓力項、擴散項、源項:
\rho(\frac{\partial V}{\partial t}+(V\cdot \triangledown )V)=-\triangledown p +\mu \triangledown^{2}V +f
對流項與擴散項對於整個流場特性尤其重要,假設流體由左至右流動,當對流效應相當明顯時,對於當下求解的網格點i而言,影響幾乎都來自左側上游網格點i – 1,如果這時使用中央差分來離散空間項,同時考慮上下游(網格點i – 1與網格點i + 1)影響的話,由於採用的離散數值方法不符合流場特性,會使得數值求解相當不穩定。
為了解決這個問題,迎風格式才被發展出來。
根據對流項係數正負來判斷流體行進方向,當常數c為正的時候,代表流體由左往右移動,由於對流效應強烈,我們只需考慮上游點i – 1的影響,採用後向差分來離散空間項;反之,當流體由右往左移動,採用前向差分來離散空間項。
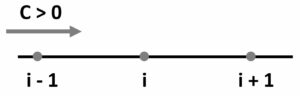
因此,迎風格式(upwind scheme)作為一種離散空間項的方法,適合用在對流主導的問題,以用來減少數值求解不穩定的情況。
主廚結語
本次簡單與各位介紹迎風格式的運作方式與特性,除了迎風格式(upwind scheme)以外,基於不同數值運算需求,也發展出各式各樣的離散格式,如何正確地使用不同離散格式也是一門學問,後續再來跟各位聊聊。
如果對這類文章有興趣的話,歡迎追蹤科技雞湯Facebook,持續關注最新消息!
