前陣子主廚在科技雞湯更新了Prof. Barba的CFD教材,該教材基於有限差分法來講解如何求解Navier-Stokes方程。問題來了,什麼是差分呢?對於數值分析的初學者而言,可能是個很陌生的名詞,本次主廚就來講講什麼叫做差分!
什麼是微分?
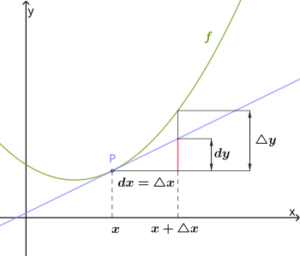
了解差分法之前,我們先來複習一下微分。所謂的微分是一種數學概念,用來描述某個函數在某一點的變化率。具體而言,對於一個連續可微函數,該函數在某一點的微分指的是當我們對該點進行極小的變動時,該函數值的變化情況。這種變化率在物理學、工程學以及其他領域都有廣泛的應用,例如速度就是距離對時間的微分。
什麼是差分?
簡單複習微分概念後,我們來看看什麼是差分。
差分是數值分析中的一個重要技術,用來逼近微分。當我們處理的函數為非連續函數,或者我們需要在電腦上近似某個微分,差分便會派上用場。差分的主要概念是取函數在兩點之間的差值來估計這段區間的平均變化率,常見的差分主要有前向差分、後向差分以及中央差分。
為了讓各位更容易理解什麼是差分,這邊實際用一個例子來講解差分法的應用。
假設我們有一個函數f(x) = x^2 並希望在x = 2處估計它的微分值。對於這個函數,實際微分式子是 {f}'=2x,所以在x = 2處的實際微分值為 4。但如果沒有這個導數公式,或者函數太過複雜而不能直接求微分,則可使用差分法來估算。
前向差分(Forward difference)
前向差分是指在函數的某點,使用該點及下一點的函數值來計算變化率。在數學上可表示為:
{f}'(x)\approx \frac{f(x+h)-f(x)}{h}
其中,h 是兩點之間的距離,而 {f}'(x)是函數在點x的差分估算。取h = 0.01,則函數f(x) = x^2的前向差分估算值為4.01。
{f}'(2)\approx \frac{f(2.01)-f(2)}{0.01} = \frac{4.0401 - 4}{0.01}=4.01
後向差分(Backward difference)
後向差分與前向差分相似,不同在於它使用前一點與當下點的函數值來估算。數學表達式為:
{f}'(x)\approx \frac{f(x)-f(x-h)}{h}
同樣取h = 0.01,則函數f(x) = x^2的後向差分估算值為3.99。
{f}'(2)\approx \frac{f(2)-f(1.99)}{0.01} = \frac{4 - 3.9601}{0.01}=3.99
中央差分(Central difference)
中央差分結合前向和後向差分的概念,它使用當下點前面與後面的函數值來估計,相較前向差分與後向差分,它的估計通常更精確。底下為其數學表達式:
{f}'(x)\approx \frac{f(x+h)-f(x-h)}{2h}
同樣取h = 0.01,則函數f(x) = x^2的後向差分估算值為4.0。
{f}'(2)\approx \frac{f(2.01)-f(1.99)}{0.02} = \frac{4.0401 - 3.9601}{0.01}=4.0
要特別注意的是,雖然這個例子裡的中央差分估算值與實際微分值相同,但這不代表中央差分每次都能準確估算微分值,仍取決於估算函數與估算採用的間距值。
差分有什麼用途?
差分在許多領域都有著廣泛的應用。其中最常見的用途是解微分方程。許多實際問題都可以用微分方程來描述。但不是所有微分方程都可以找到解析解,在這些情況下,可以使用差分法來逼近這些方程的解。此外,差分也能用於數據分析中的趨勢預測、經濟學的時間序列分析以及圖像處理的邊緣檢測等多種應用。
主廚結語
本次與各位簡單介紹差分基本概念與常見的差分類型,由於描述流體運動的Navier-Stokes方程尚未發現解析解,差分法就成了計算流體力學中相當重要的概念。此次僅介紹一次微分作為例子,那如果是二次微分的情況下,該如何用差分法估算呢?各位可以試著想想看喔!