流體拓樸優化概念與原理

在《拓樸最佳化基本介紹與應用發展》一文中曾經與大家介紹拓樸優化的基本概念，本文將會延續這篇文章的內容，基於Thomas Borrvall於2003年發表的論文《Topology optimization of fluids in Stokes flow》，為大家介紹流體拓樸優化的基本原理。

流體拓樸優化基本原理

在介紹流體拓樸優化前，先替各位簡單溫習一下什麼是拓樸優化。在一定的設計空間下，根據給定的限制條件與目標函數，找出滿足目標函數的拓樸結構設計，此為拓樸最佳化的基本概念，圖1展示優化流程並呈現固定樑在中央受力且減重50%的情況下的優化結構。

圖1 拓樸最佳化流程圖[2]

簡單了解什麼是拓樸優化後，我們來看看流體拓樸優化的基本原理。考慮一個不可壓縮的牛頓理想流體，其連續方程式與動量方程式可表示成下式：

$\triangledown \cdot v=0 - (1)$

$\rho(\frac{\partial v}{\partial t}+(v\cdot \triangledown )v)=-\triangledown p +\mu \triangledown^{2}v +f - (2)$

其中v為速度，p為壓力，ρ為密度，t為時間，μ為黏滯度，f為源項。為了求解優化結構，我們必須決定設計區域內的元素屬於可流動的流體空間還是不可流動的固體空間，既然每個元素只有兩種狀態，只要將所有的排列組合都求解出來，不就可以找到最佳解了嗎？

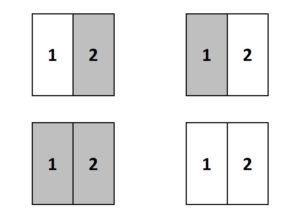
我們來想想看這樣會發生什麼事，當設計區域的元素數量等於1的時候，只有固體或液體兩種組合，而當區域內元素增加到2個的時候，便有固固、固液、液固、液液四種組合，如圖2。從上述推論可知，當設計區域內元素N個的時候共有2的N次方種組合，求解所有組合來找最佳構形顯然不太實際。

既然這方法不可行，那我們應該要怎麼做呢？

上述思路是以離散角度來看待最佳化問題，若能將問題轉換成連續可求導的形式，便能基於導數資訊來執行最佳化演算法。為了達成這個目的，原先只有液態跟固態兩種狀態的元素，改以密度表示，元素密度為0的時候為固體，密度為1的時候為液體，而密度在此作為設計變數，在0 – 1之間具有連續性。

定義設計變數後，下一步就是要關聯設計變數與求解方程式，因此將式2的Navier-Stokes方程改寫成下列形式，其中α為inverse permeability。透過額外添加的源項來關聯設計變數與求解方程式，求得目標函數對設計變數的導數後，就能基於敏感度資訊來求解流體拓樸優化問題。

$\rho(\frac{\partial v}{\partial t}+(v\cdot \triangledown )v)=-\triangledown p +\mu \triangledown^{2}v - \alpha v - (3)$

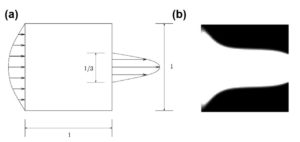
Thomas Borrvall 的論文中實作了幾個經典案例，其中一個為Diffuser算例，其邊界條件與設計區域如圖3(a)所示，設計區域左側為速度入口，右側中央開口為速度出口，若以流體能量耗散最小化為目標函數，流道體積為設計區域體積50%的情況下，優化流道如圖3(b)所示。

為了讓各位對拓樸優化的迭代過程更有感覺，底下為主廚在體積約束為設計區域70%的情況下求解Diffuser案例的過程，從影片可以看到優化流道會隨著迭代過程慢慢成形。

本次與各位介紹流體拓樸優化的基本思路，不知各位覺得如何呢？雖然流體拓樸優化是個新興研究領域，但相當具有應用潛力，期許未來能看到這項技術發光發熱的一天！若對這類文章有興趣的話，可以追蹤科技雞湯的Facebook，追蹤最新消息！

Thomas Borrvall et al., Topology optimization of fluids in Stokes flow, Numerical Methods in Fluids 2003, 41(1), 77 – 107
Martin P. Bendsøe, Ole Sigmund, Topology Optimization Theory, Methods, and Applications, 2004