(本文經Prof. Lorena A. Barba授權轉載翻譯自Prof. Lorena A. Barba的教材”12 Steps to Navier-Stokes”,原文鏈結請參照底下參考資料)
Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved BSD-3 license. (c) Lorena A. Barba, Gilbert F. Forsyth 2017. Thanks to NSF for support via CAREER award #1149784.
CFD Python:求解Navier-Stokes方程的12個步驟(1) CFD Python:求解Navier-Stokes方程的12個步驟(2) CFD Python:求解Navier-Stokes方程的12個步驟(3) CFD Python:求解Navier-Stokes方程的12個步驟(4) CFD Python:求解Navier-Stokes方程的12個步驟(5) CFD Python:求解Navier-Stokes方程的12個步驟(6) CFD Python:求解Navier-Stokes方程的12個步驟(7) CFD Python:求解Navier-Stokes方程的12個步驟(8) CFD Python:求解Navier-Stokes方程的12個步驟(9) CFD Python:求解Navier-Stokes方程的12個步驟(10) CFD Python:求解Navier-Stokes方程的12個步驟(11) CFD Python:求解Navier-Stokes方程的12個步驟(12)
哈囉!歡迎來到求解Naiver-Stokes方程的教學,這是波士頓大學教授Lorena A. Barba從2009年春季於計算流體力學課程上教學的程式模組。這項課程假定您已具有基本程式能力(任何程式語言)以及偏微分方程與流體力學相關基礎知識。
此程式模組出自 Rio Yokota博士的主意(Barba研究室的後博士研究員),並由Barba教授與其學生在幾個學期的課程教學中不斷完善,此課程完全使用Pyhton教學,不懂Pyhton的學生也能透過此教程來學習。
這系列教學將會從零開始帶您從第一個步驟寫出自己的Navier-Stokes方程求解器,而我們即將開始。如果一開始什麼都不懂也不用擔心,我們將在接下來的過程中為您講解,而您也能透過Prof. Barba’s lectures on YouTube的影片來學習。
步驟1:一維線性對流方程
一維線性對流方程式是能用來學習CFD的基本模型。一個簡單的方程式能學到這麼多真令人驚喜,該方程如下:
\frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = 0
加上給定的初始條件(可理解為波),該方程式代表初始條件給定的波以速度c傳遞,且波形不變。假設初始條件為u(x,0)=u_0(x),則方程式精確解為u(x,t)=u_0(x-ct)。
我們使用前向差分來離散此方程的時間項,並用後向差分來離散空間項。離散的空間座標x用索引i = 0 至 N來表示,且離散後的時間步階以尺寸\Delta t表示
從微分定義來看可以得知:
\frac{\partial u}{\partial x}\approx \frac{u(x+\Delta x)-u(x)}{\Delta x}
因此,離散方程可寫成如下形式:
\frac{u_i^{n+1}-u_i^n}{\Delta t} + c \frac{u_i^n - u_{i-1}^n}{\Delta x} = 0
其中n與n+1代表時間上連續的兩個步階,而i – 1與i代表X方向上離散座標的兩個相鄰點。如果有給定的初始條件,那麼離散方程式的未知數就只有u_i^{n+1}。因此,能夠以一個隨著時間推進的方程式來求解未知數,如下:
u_i^{n+1} = u_i^n - c \frac{\Delta t}{\Delta x}(u_i^n-u_{i-1}^n)
現在嘗試用Python來實踐它。
首先必須引入一些新的函式庫來幫助我們:
- numpy是一個提供許多矩陣操作的函式庫,類似MATLAB
- matplotlib是一個2D繪圖函式庫用來幫我們畫出結果
- time and sys提供基本的時間函式來幫助我們放慢動畫以便觀察結果
# Remember: comments in python are denoted by the pound sign
import numpy #here we load numpy
from matplotlib import pyplot #here we load matplotlib
import time, sys #and load some utilities #this makes matplotlib plots appear in the notebook (instead of a separate window)
%matplotlib inline 現在來定義一些新變數,我們想要在長度2的空間中定義等間距的網格點,因此x_i\in(0,2)。變數 nx表示網格點數量,且變數dx為任意一組兩個相鄰網格點的間距。
nx = 41 # try changing this number from 41 to 81 and Run All ... what happens?
dx = 2 / (nx-1)
nt = 25 #nt is the number of timesteps we want to calculate
dt = .025 #dt is the amount of time each timestep covers (delta t)
c = 1 #assume wavespeed of c = 1此外,也需要設置初始條件。初始速度u_0在間距0.5 \leq x \leq 1給定u = 2,並在(0, 2)的任意某處皆為 u = 1(此為hat function)。
這邊使用函式ones()來定義一個numpy的陣列,該陣列有著nx元素且各項元素值為1。
u = numpy.ones(nx) #numpy function ones()
u[int(.5 / dx):int(1 / dx + 1)] = 2 #setting u = 2 between 0.5 and 1 as per our I.C.s
print(u)現在用matplotlib的plot功能來看看初始條件。我們已經引入matplotlib的繪圖庫pyplot且繪圖函式為plot,因此可以呼叫pyplot.plot。如果想要學習更多matplotlib,可參考有著範例繪圖的網站。
這裡使用簡單的二維繪圖語法: plot(x, y),其中x為均分網格節點:
pyplot.plot(numpy.linspace(0, 2, nx), u);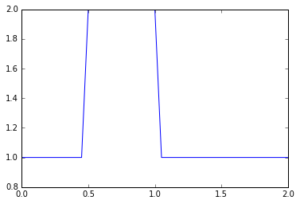
為什麼帽函式(hat function)沒出現完美的直線?可以稍微思考看看。
現在是時候用有限差分來離散對流方程,對於陣列每個元素而言,我們需要執行下列操作
u_i^{n+1} = u_i^n - c \frac{\Delta t}{\Delta x}(u_i^n-u_{i-1}^n)
把計算結果儲存在新(暫存)的陣列un,而un會做為下個時間步的u來計算。我們會不斷重複此操作,直到有足夠的時間步來讓我們觀察波動如何傳遞。
我們先用Numpy函式ones()來初始化陣列un,陣列un用來保存第n+1個時間步的數值。
這邊可能有兩個迭代操作:一個是空間上的迭代,另一個是時間上的迭代,因此我們將會以巢狀迴圈的寫法來實踐。注意range()函式的使用,當我們寫for i in range(1,nx),雖然會迭代整個陣列u,卻會略過第一個元素(編號0的元素),這是為什麼呢?
un = numpy.ones(nx) #initialize a temporary array
for n in range(nt): #loop for values of n from 0 to nt, so it will run nt times
un = u.copy() ##copy the existing values of u into un
for i in range(1, nx): ## you can try commenting this line and...
#for i in range(nx): ## ... uncommenting this line and see what happens!
u[i] = un[i] - c * dt / dx * (un[i] - un[i-1])我們稍後會知道上述程式碼效率很差,在Python還有著更好的寫法,不過先繼續學習。
現在來試著畫出隨著時間推進後的陣列u。
pyplot.plot(numpy.linspace(0, 2, nx), u);
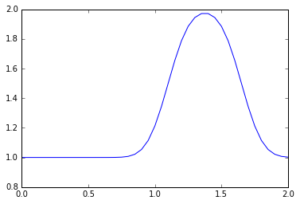
參考資料
- 12 steps to Navier–Stokes: Step 1: 1-D Linear Convection,Lorena A. Barba

本著作係採用創用 CC 姓名標示 4.0 國際 授權條款授權.
