(本文經Prof. Lorena A. Barba授權轉載翻譯自Prof. Lorena A. Barba的教材”12 Steps to Navier-Stokes”,原文鏈結請參照底下參考資料)
Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved BSD-3 license. (c) Lorena A. Barba, Gilbert F. Forsyth 2017. Thanks to NSF for support via CAREER award #1149784.
CFD Python:求解Navier-Stokes方程的12個步驟(1) CFD Python:求解Navier-Stokes方程的12個步驟(2) CFD Python:求解Navier-Stokes方程的12個步驟(3) CFD Python:求解Navier-Stokes方程的12個步驟(4) CFD Python:求解Navier-Stokes方程的12個步驟(5) CFD Python:求解Navier-Stokes方程的12個步驟(6) CFD Python:求解Navier-Stokes方程的12個步驟(7) CFD Python:求解Navier-Stokes方程的12個步驟(8) CFD Python:求解Navier-Stokes方程的12個步驟(9) CFD Python:求解Navier-Stokes方程的12個步驟(10) CFD Python:求解Navier-Stokes方程的12個步驟(11) CFD Python:求解Navier-Stokes方程的12個步驟(12)
步驟4:Burgers’ 方程式
您可以在維基頁面閱讀Burgers’方程式的相關資料。一維Burgers’方程式如下所示:
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = \nu \frac{\partial ^2u}{\partial x^2}
如同你所見,Burger’s方程結合了非線性對流項與擴散項。令人驚訝的是,你將會從這個小小的方程式學到許多東西!
我們可以藉由先前步驟1至步驟3的方法來離散此方程式。時間項離散採用前向差分,空間項離散採用後向差分並使用二次項的離散方法來離散二次微分項,離散形式如下:
\frac{u_i^{n+1}-u_i^n}{\Delta t} + u_i^n \frac{u_i^n - u_{i-1}^n}{\Delta x} = \nu \frac{u_{i+1}^n - 2u_i^n + u_{i-1}^n}{\Delta x^2}
如同之前幾個步驟,一旦有了初始條件,唯一的未知項就只有u_i^{n+1}。將方程式改寫成隨著時間推進的形式如下:
u_i^{n+1} = u_i^n - u_i^n \frac{\Delta t}{\Delta x} (u_i^n - u_{i-1}^n) + \nu \frac{\Delta t}{\Delta x^2}(u_{i+1}^n - 2u_i^n + u_{i-1}^n)
初始條件與邊界條件
為了觀察一些Burger’s方程式的有趣特性,採用與先前步驟不同的初始條件與邊界條件會很有幫助。初始條件如下:
u = -\frac{2 \nu}{\phi} \frac{\partial \phi}{\partial x} + 4 -(1)
\phi = \exp \bigg(\frac{-x^2}{4 \nu} \bigg) + \exp \bigg(\frac{-(x-2 \pi)^2}{4 \nu} \bigg) -(2)
基於這個初始條件,解析解給定如下:
u = -\frac{2 \nu}{\phi} \frac{\partial \phi}{\partial x} + 4 -(3)
\phi = \exp \bigg(\frac{-(x-4t)^2}{4 \nu (t+1)} \bigg) + \exp \bigg(\frac{-(x-4t -2 \pi)^2}{4 \nu(t+1)} \bigg) -(4)
邊界條件如下:
u(0) = u(2\pi)此邊界條件稱為週期性邊界條件。注意!如果沒有處理好這個邊界條件會讓您有點困擾!
使用Sympy來節省時間
如果手算用於Burger’s方程式的初始條件會有些痛苦,導數\frac{\partial \phi}{\partial x}的計算並不是很困難,但很容易漏掉符號或是忘記某處X的因素,因此使用函式庫SymPy來幫助我們。
SymPy是一個符號計算的Python函式庫。它有許多跟Mathematica相同的符號數學計算功能,還有個好處是能將結果轉換至Python計算(同樣是免費開源的)。
首先載入SymPy函式庫與我們常用的另一個函式庫Numpy。
import numpy
import sympy我們要告訴SymPy它的輸出需要使用LATEX來做編排,那會讓輸出更加漂亮!
from sympy import init_printing
init_printing(use_latex=True)先設置初始條件的三個符號變數,接著寫出關於\phi完整的方程式,執行後應該會得到一個精心編排過的\phi方程式。
x, nu, t = sympy.symbols('x nu t')
phi = (sympy.exp(-(x - 4 * t)**2 / (4 * nu * (t + 1))) +
sympy.exp(-(x - 4 * t - 2 * sympy.pi)**2 / (4 * nu * (t + 1))))
phi
也許輸出的方程式看起來有點小,不過是正確的。現在評估偏微分導數\frac{\partial \phi}{\partial x}變得很容易。
phiprime = phi.diff(x)
phiprime- \frac{e^{- \frac{\left(- 4 t + x\right)^{2}}{4 \nu \left(t + 1\right)}}}{4 \nu \left(t + 1\right)} \left(- 8 t + 2 x\right) - \frac{1}{4 \nu \left(t + 1\right)} \left(- 8 t + 2 x - 4 \pi\right) e^{- \frac{\left(- 4 t + x - 2 \pi\right)^{2}}{4 \nu \left(t + 1\right)}}
如果想看沒有編排過的版本,只要使用Python中的print指令。
print(phiprime)-(-8*t + 2*x)*exp(-(-4*t + x)**2/(4*nu*(t + 1)))/(4*nu*(t + 1)) - (-8*t + 2*x - 4*pi)*exp(-(-4*t + x - 2*pi)**2/(4*nu*(t + 1)))/(4*nu*(t + 1))
現在該怎麼辦?
現在我們擁有Python版本的導數,可以寫出完整的初始條件並把它轉換成有用的Python敘述式。因此,我們使用lambdify函式,它採用SymPy的符號方程並將它轉換成可呼叫的函式。
from sympy.utilities.lambdify import lambdify
u = -2 * nu * (phiprime / phi) + 4
print(u)-2*nu*(-(-8*t + 2*x)*exp(-(-4*t + x)**2/(4*nu*(t + 1)))/(4*nu*(t + 1)) - (-8*t + 2*x - 4*pi)*exp(-(-4*t + x - 2*pi)**2/(4*nu*(t + 1)))/(4*nu*(t + 1)))/(exp(-(-4*t + x - 2*pi)**2/(4*nu*(t + 1))) + exp(-(-4*t + x)**2/(4*nu*(t + 1)))) + 4
Lambdify
為了讓這個表達式lambdify後變成一個有用的函式,必須告訴lambdify需要哪些變數以及要插入它們的函式。
ufunc = lambdify((t, x, nu), u)
print(ufunc(1, 4, 3))3.49170664206
回到Burger’s 方程式
現在已經設置初始條件,可以繼續完成這個問題,而我們也能用lambdify函式來生成初始條件的圖。
from matplotlib import pyplot
%matplotlib inline
###variable declarations
nx = 101
nt = 100
dx = 2 * numpy.pi / (nx - 1)
nu = .07
dt = dx * nu
x = numpy.linspace(0, 2 * numpy.pi, nx)
un = numpy.empty(nx)
t = 0
u = numpy.asarray([ufunc(t, x0, nu) for x0 in x])
uarray([ 4. , 4.06283185, 4.12566371, 4.18849556, 4.25132741, 4.31415927, 4.37699112, 4.43982297, 4.50265482, 4.56548668, 4.62831853, 4.69115038, 4.75398224, 4.81681409, 4.87964594, 4.9424778 , 5.00530965, 5.0681415 , 5.13097336, 5.19380521, 5.25663706, 5.31946891, 5.38230077, 5.44513262, 5.50796447, 5.57079633, 5.63362818, 5.69646003, 5.75929189, 5.82212374, 5.88495559, 5.94778745, 6.0106193 , 6.07345115, 6.136283 , 6.19911486, 6.26194671, 6.32477856, 6.38761042, 6.45044227, 6.51327412, 6.57610598, 6.63893783, 6.70176967, 6.76460125, 6.82742866, 6.89018589, 6.95176632, 6.99367964, 6.72527549, 4. , 1.27472451, 1.00632036, 1.04823368, 1.10981411, 1.17257134, 1.23539875, 1.29823033, 1.36106217, 1.42389402, 1.48672588, 1.54955773, 1.61238958, 1.67522144, 1.73805329, 1.80088514, 1.863717 , 1.92654885, 1.9893807 , 2.05221255, 2.11504441, 2.17787626, 2.24070811, 2.30353997, 2.36637182, 2.42920367, 2.49203553, 2.55486738, 2.61769923, 2.68053109, 2.74336294, 2.80619479, 2.86902664, 2.9318585 , 2.99469035, 3.0575222 , 3.12035406, 3.18318591, 3.24601776, 3.30884962, 3.37168147, 3.43451332, 3.49734518, 3.56017703, 3.62300888, 3.68584073, 3.74867259, 3.81150444, 3.87433629, 3.93716815, 4. ])
pyplot.figure(figsize=(11, 7), dpi=100)
pyplot.plot(x, u, marker='o', lw=2)
pyplot.xlim([0, 2 * numpy.pi])
pyplot.ylim([0, 10]);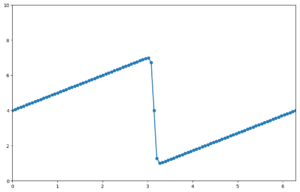
這絕不是迄今為止都在處理的帽函式(hat function),這邊將它稱為”鋸齒函式”(saw-tooth function),我們繼續往下看會發生什麼。
週期性邊界條件
步驟4與前面幾個步驟最大的差異在於週期性邊界條件。如果你有實際跑過步驟1與步驟2的程式並讓模擬跑得更久(透過增加 nt),你會得知波動將持續往右邊前行直到它不再出現。透過週期性邊界條件,當點移動至右側邊界後,它會再繞回前面邊界。
回想我們在這個步驟實作的離散方程式:
u_i^{n+1} = u_i^n - u_i^n \frac{\Delta t}{\Delta x} (u_i^n - u_{i-1}^n) + \nu \frac{\Delta t}{\Delta x^2}(u_{i+1}^n - 2u_i^n + u_{i-1}^n)
當點i位在邊界尾端的時候,u_{i+1}^n代表什麼呢?在繼續學習前先想個一分鐘。
for n in range(nt):
un = u.copy()
for i in range(1, nx-1):
u[i] = un[i] - un[i] * dt / dx *(un[i] - un[i-1]) + nu * dt / dx**2 *\
(un[i+1] - 2 * un[i] + un[i-1])
u[0] = un[0] - un[0] * dt / dx * (un[0] - un[-2]) + nu * dt / dx**2 *\
(un[1] - 2 * un[0] + un[-2])
u[-1] = u[0]
u_analytical = numpy.asarray([ufunc(nt * dt, xi, nu) for xi in x])pyplot.figure(figsize=(11, 7), dpi=100)
pyplot.plot(x,u, marker='o', lw=2, label='Computational')
pyplot.plot(x, u_analytical, label='Analytical')
pyplot.xlim([0, 2 * numpy.pi])
pyplot.ylim([0, 10])
pyplot.legend();
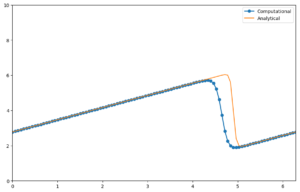
下個學習階段是?
接下來的步驟5到步驟12將會是二維問題。但這只是簡單地將一維有限差分應用在二維與三維的偏導數。只需要使用這個定義 ─ x的偏導數只是當y保持定量時沿著x方向的變量而已。
進到步驟5之前,確定你已經完成步驟1至步驟4的程式碼,而且已試驗過各種參數並看過結果。此外,我們也推薦你可以稍微學一下Numpy的矩陣操作。
參考資料
- 12 steps to Navier–Stokes: Step 4: Burgers’ Equation,Lorena A. Barba

本著作係採用創用 CC 姓名標示 4.0 國際 授權條款授權.
