(本文經Prof. Lorena A. Barba授權轉載翻譯自Prof. Lorena A. Barba的教材”12 Steps to Navier-Stokes”,原文鏈結請參照底下參考資料)
Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved BSD-3 license. (c) Lorena A. Barba, Gilbert F. Forsyth 2017. Thanks to NSF for support via CAREER award #1149784.
CFD Python:求解Navier-Stokes方程的12個步驟(1) CFD Python:求解Navier-Stokes方程的12個步驟(2) CFD Python:求解Navier-Stokes方程的12個步驟(3) CFD Python:求解Navier-Stokes方程的12個步驟(4) CFD Python:求解Navier-Stokes方程的12個步驟(5) CFD Python:求解Navier-Stokes方程的12個步驟(6) CFD Python:求解Navier-Stokes方程的12個步驟(7) CFD Python:求解Navier-Stokes方程的12個步驟(8) CFD Python:求解Navier-Stokes方程的12個步驟(9) CFD Python:求解Navier-Stokes方程的12個步驟(10) CFD Python:求解Navier-Stokes方程的12個步驟(11) CFD Python:求解Navier-Stokes方程的12個步驟(12)
到目前為止,全部的練習都是在一維空間。我們可以從一維例題學到許多,不過讓我們朝下個目標邁進:二維問題。
在下面的練習中,你將會把前四個步驟擴展至二維問題。要將一維有限差分公式運用至二維或三維,只需要應用這個定義:x的偏導數只是當y保持定量時沿著x方向的變量而已。
在二維空間中,一個矩形(均勻)網格透過下列座標點定義:
x_i = x_0 +i \Delta x
y_i = y_0 +i \Delta y
現在定義u_{i,j} = u(x_i,y_j),針對任一變量x, y來應用有限差分公式,分別作用於i索引與j索引。所有導數都基於作用在網格點u_{i,j}周圍的二維泰勒展開式。
因此,對於x方向上的一維偏導數而言,有限差分式子如下:
\frac{\partial u}{\partial x}\biggr\rvert_{i,j} = \frac{u_{i+1,j}-u_{i,j}}{\Delta x}+\mathcal{O}(\Delta x)
而在y方向上也有類似的公式。因此,我們可以寫出步驟5至12前向差分、後向差分以及中央差分的公式。讓我們開始吧!
步驟5:二維線性對流
二維線性對流方程如下:
\frac{\partial u}{\partial t}+c\frac{\partial u}{\partial x} + c\frac{\partial u}{\partial y} = 0
這確實與我們一維線性對流方程相同,撇除我們擁有兩個需要隨著時間推進的空間項。與先前一樣,時間步長使用前向差分離散,空間項使用後向差分離散。
在一維的案例實作,我們使用i作為下標來表示空間項變化(e.g. u_{i}^n-u_{i-1}^n)。現在我們必須考慮二維,因此添加第二個下標j來表示二維空間資訊。
這裡一樣使用i作為x方向的索引,而j下標則用來追蹤y方向。把這個銘記在心,偏微分方程的離散將會變得相對直覺許多。
\frac{u_{i,j}^{n+1}-u_{i,j}^n}{\Delta t} + c\frac{u_{i, j}^n-u_{i-1,j}^n}{\Delta x} + c\frac{u_{i,j}^n-u_{i,j-1}^n}{\Delta y}=0
跟之前一樣,可用下式求解未知項:
u_{i,j}^{n+1} = u_{i,j}^n-c \frac{\Delta t}{\Delta x}(u_{i,j}^n-u_{i-1,j}^n)-c \frac{\Delta t}{\Delta y}(u_{i,j}^n-u_{i,j-1}^n)
我們將會搭配下述初始條件來求解這個方程式:
u(x,y) = \begin{cases} \begin{matrix} 2\ \text{for} & 0.5 \leq x, y \leq 1 \cr 1\ \text{for} & \text{everywhere else}\end{matrix}\end{cases}
以及考慮下述邊界條件:
u = 1\ \text{for } \begin{cases} \begin{matrix} x = 0,\ 2 \cr y = 0,\ 2 \end{matrix}\end{cases}
from mpl_toolkits.mplot3d import Axes3D ##New Library required for projected 3d plots import numpy from matplotlib import pyplot, cm %matplotlib inline###variable declarations nx = 81 ny = 81 nt = 100 c = 1 dx = 2 / (nx - 1) dy = 2 / (ny - 1) sigma = .2 dt = sigma * dx x = numpy.linspace(0, 2, nx) y = numpy.linspace(0, 2, ny) u = numpy.ones((ny, nx)) ##create a 1xn vector of 1's un = numpy.ones((ny, nx)) ## ###Assign initial conditions ##set hat function I.C. : u(.5<=x<=1 && .5<=y<=1 ) is 2 u[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2 ###Plot Initial Condition ##the figsize parameter can be used to produce different sized images fig = pyplot.figure(figsize=(11, 7), dpi=100) ax = fig.gca(projection='3d') X, Y = numpy.meshgrid(x, y) surf = ax.plot_surface(X, Y, u[:], cmap=cm.viridis)
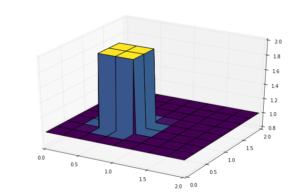
3D繪圖註記
為了繪製3D投影結果,請確保您已添加Axes3D函式庫。
from mpl_toolkits.mplot3d import Axes3D實際的繪圖指令比簡單2D繪圖還要複雜一些。
fig = pyplot.figure(figsize=(11, 7), dpi=100)
ax = fig.gca(projection='3d')
surf2 = ax.plot_surface(X, Y, u[:])這裡的第一行指令用來初始化繪圖視窗。figsize指令與dpi指令為額外選項,只是用來指定圖形尺寸與解析度。你可以忽略他們,但你仍需要底下指令:
fig = pyplot.figure()下一行將軸標籤’ax’指定給繪圖視窗並表示這會是個3D投影繪圖。最後一行使用下列指令:
plot_surface()這一行等同一般繪圖指令,但它使用X與Y網格點數據來表示資料點位置。
註記
傳給plot_surface的X值與Y值並不是X與Y的一維向量。為了使用matplotlibs的3D繪圖功能,你必須產生基於x值與y值的網格且該網格對應於繪圖窗口中的每個座標。該網格可用numpy功能meshgrid產生。
X, Y = numpy.meshgrid(x, y)二維空間迭代
為了評估二維中的波動,需要使用涵蓋i與j的巢狀迴圈。由於Python並不是編譯語言,執行多重迴圈程式碼的速度將會明顯下降。首先,先用來嘗試評估二維對流的程式碼並看看會產生什麼結果。
u = numpy.ones((ny, nx))
u[int(.5 / dy):int(1 / dy + 1), int(.5 / dx):int(1 / dx + 1)] = 2
for n in range(nt + 1): ##loop across number of time steps
un = u.copy()
row, col = u.shape
for j in range(1, row):
for i in range(1, col):
u[j, i] = (un[j, i] - (c * dt / dx * (un[j, i] - un[j, i - 1])) -
(c * dt / dy * (un[j, i] - un[j - 1, i])))
u[0, :] = 1
u[-1, :] = 1
u[:, 0] = 1
u[:, -1] = 1
fig = pyplot.figure(figsize=(11, 7), dpi=100)
ax = fig.gca(projection='3d')
surf2 = ax.plot_surface(X, Y, u[:], cmap=cm.viridis)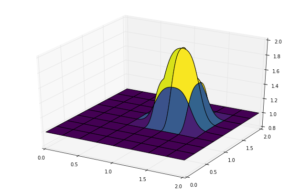
矩陣操作
這裡同樣有個二維對流程式碼,然而這段程式碼並不是使用巢狀迴圈,而是利用矩陣操作來執行同樣計算。
u = numpy.ones((ny, nx))
u[int(.5 / dy):int(1 / dy + 1), int(.5 / dx):int(1 / dx + 1)] = 2
for n in range(nt + 1): ##loop across number of time steps
un = u.copy()
u[1:, 1:] = (un[1:, 1:] - (c * dt / dx * (un[1:, 1:] - un[1:, :-1])) -
(c * dt / dy * (un[1:, 1:] - un[:-1, 1:])))
u[0, :] = 1
u[-1, :] = 1
u[:, 0] = 1
u[:, -1] = 1
fig = pyplot.figure(figsize=(11, 7), dpi=100)
ax = fig.gca(projection='3d')
surf2 = ax.plot_surface(X, Y, u[:], cmap=cm.viridis)
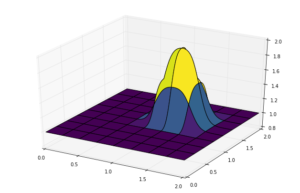
參考資料
- 12 steps to Navier–Stokes: Step 5: 2-D Linear Convection,Lorena A. Barba

本著作係採用創用 CC 姓名標示 4.0 國際 授權條款授權.
