(本文經Prof. Lorena A. Barba授權轉載翻譯自Prof. Lorena A. Barba的教材”12 Steps to Navier-Stokes”,原文鏈結請參照底下參考資料)
Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved BSD-3 license. (c) Lorena A. Barba, Gilbert F. Forsyth 2017. Thanks to NSF for support via CAREER award #1149784.
CFD Python:求解Navier-Stokes方程的12個步驟(1) CFD Python:求解Navier-Stokes方程的12個步驟(2) CFD Python:求解Navier-Stokes方程的12個步驟(3) CFD Python:求解Navier-Stokes方程的12個步驟(4) CFD Python:求解Navier-Stokes方程的12個步驟(5) CFD Python:求解Navier-Stokes方程的12個步驟(6) CFD Python:求解Navier-Stokes方程的12個步驟(7) CFD Python:求解Navier-Stokes方程的12個步驟(8) CFD Python:求解Navier-Stokes方程的12個步驟(9) CFD Python:求解Navier-Stokes方程的12個步驟(10) CFD Python:求解Navier-Stokes方程的12個步驟(11) CFD Python:求解Navier-Stokes方程的12個步驟(12)
請回想一下不可壓縮流體的Naiver-Stokes方程,其中\vec{v}表示速度場:
\nabla \cdot\vec{v} = 0
\frac{\partial \vec{v}}{\partial t}+(\vec{v}\cdot\nabla)\vec{v} = -\frac{1}{\rho}\nabla p + \nu \nabla^2\vec{v}
第一個方程表示恆定密度下的質量守恆。第二個方程是動量守恆。但是出現了一個問題:不可壓縮流的連續方程沒有主要變數,也沒有明顯的方法來耦合速度和壓力。相比之下,可壓縮流的質量連續性為密度ρ提供一個演化方程,它耦合了關於ρ和p的狀態方程。
在不可壓縮流中,連續方程\nabla \cdot\vec{v} = 0提供一個動力上的約束,要求壓力場隨著膨脹率\nabla \cdot\vec{v} = 0消失而演變。為了耦合速度與壓力,解決方法是構建一個壓力場來滿足連續性,對動量方程求取散度,進而得到壓力的泊松方程(Poisson equation)!
步驟10:2D泊松方程(Poisson equation)
泊松方程是透過在Laplace方程右側加上一個源項而得到:
\frac{\partial ^2 p}{\partial x^2} + \frac{\partial ^2 p}{\partial y^2} = b
因此,與Laplace方程不同,場內有一個有限值影響解。泊松方程起到”鬆弛”場內初始源的作用。而泊松方程的離散形式看起來幾乎與步驟9相同,只是多了源項:
\frac{p_{i+1,j}^{n}-2p_{i,j}^{n}+p_{i-1,j}^{n}}{\Delta x^2}+\frac{p_{i,j+1}^{n}-2 p_{i,j}^{n}+p_{i,j-1}^{n}}{\Delta y^2}=b_{i,j}^{n}
與先前一樣,重新排列這個方程,以便在點i,j處獲得p。因此得到:
p_{i,j}^{n}=\frac{(p_{i+1,j}^{n}+p_{i-1,j}^{n})\Delta y^2+(p_{i,j+1}^{n}+p_{i,j-1}^{n})\Delta x^2-b_{i,j}^{n}\Delta x^2\Delta y^2}{2(\Delta x^2+\Delta y^2)}
假設初始狀態所有地方的p=0,並使用邊界條件如下:
x=0,2和y=0,1的p = 0
源項包括域內的兩個初始尖峰,如下所示:
b_{i,j}=100 在 i=\frac{1}{4}nx, j=\frac{1}{4}ny
b_{i,j}=-100 在 i=\frac{3}{4}nx, j=\frac{3}{4}ny
b_{i,j}=0 在其他地方
迭代將在偽時間推進下來鬆弛初始尖峰,而泊松方程的鬆弛變得越來越慢。為什麼?
看看泊松方程可能的程式碼寫法。像往常一樣,載入我們最愛的Python函式庫。我們還想做一些可愛的3D圖,於是定義參數並完成初始化。你對下面的方法有什麼看法?
import numpy
from matplotlib import pyplot, cm
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline# Parameters
nx = 50
ny = 50
nt = 100
xmin = 0
xmax = 2
ymin = 0
ymax = 1
dx = (xmax - xmin) / (nx - 1)
dy = (ymax - ymin) / (ny - 1)
# Initialization
p = numpy.zeros((ny, nx))
pd = numpy.zeros((ny, nx))
b = numpy.zeros((ny, nx))
x = numpy.linspace(xmin, xmax, nx)
y = numpy.linspace(xmin, xmax, ny)
# Source
b[int(ny / 4), int(nx / 4)] = 100
b[int(3 * ny / 4), int(3 * nx / 4)] = -100有了這個,我們打算透過偽時間來推進初始的猜測值。下方程式碼與步驟9用於求解Laplace方程的函式有何不同?
for it in range(nt):
pd = p.copy()
p[1:-1,1:-1] = (((pd[1:-1, 2:] + pd[1:-1, :-2]) * dy**2 +
(pd[2:, 1:-1] + pd[:-2, 1:-1]) * dx**2 -
b[1:-1, 1:-1] * dx**2 * dy**2) /
(2 * (dx**2 + dy**2)))
p[0, :] = 0
p[ny-1, :] = 0
p[:, 0] = 0
p[:, nx-1] = 0也許可以重用步驟9中的繪圖函式,你認為呢?
def plot2D(x, y, p):
fig = pyplot.figure(figsize=(11, 7), dpi=100)
ax = fig.gca(projection='3d')
X, Y = numpy.meshgrid(x, y)
surf = ax.plot_surface(X, Y, p[:], rstride=1, cstride=1, cmap=cm.viridis,
linewidth=0, antialiased=False)
ax.view_init(30, 225)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')plot2D(x, y, p)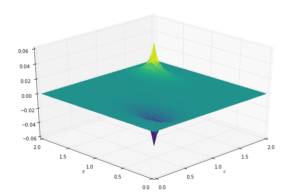
這是程式碼重複使用的驚奇!
現在,你可能會想:好吧,如果寫了這麼一個小巧的函式,它做了一些非常有用的事情,我想一遍又一遍使用它。我如何在不每次複製貼上的情況做到這一點?
如果你對此非常好奇,那麼你需要學習有關封裝(packaging)的知識。但這已經超出了我們CFD課程範疇。如果你真的想知道,就得自己去查找了。
參考資料
- 12 steps to Navier–Stokes: Step 10: 2D Poisson Equation,Lorena A. Barba

本著作係採用創用 CC 姓名標示 4.0 國際 授權條款授權.
