(本文經Prof. Lorena A. Barba授權轉載翻譯自Prof. Lorena A. Barba的教材”12 Steps to Navier-Stokes”,原文鏈結請參照底下參考資料)
Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved BSD-3 license. (c) Lorena A. Barba, Gilbert F. Forsyth 2017. Thanks to NSF for support via CAREER award #1149784.
CFD Python:求解Navier-Stokes方程的12個步驟(1) CFD Python:求解Navier-Stokes方程的12個步驟(2) CFD Python:求解Navier-Stokes方程的12個步驟(3) CFD Python:求解Navier-Stokes方程的12個步驟(4) CFD Python:求解Navier-Stokes方程的12個步驟(5) CFD Python:求解Navier-Stokes方程的12個步驟(6) CFD Python:求解Navier-Stokes方程的12個步驟(7) CFD Python:求解Navier-Stokes方程的12個步驟(8) CFD Python:求解Navier-Stokes方程的12個步驟(9) CFD Python:求解Navier-Stokes方程的12個步驟(10) CFD Python:求解Navier-Stokes方程的12個步驟(11) CFD Python:求解Navier-Stokes方程的12個步驟(12)
步驟7:二維擴散方程
底下為二維擴散方程式:
\frac{\partial u}{\partial t} = \nu \frac{\partial ^2 u}{\partial x^2} + \nu \frac{\partial ^2 u}{\partial y^2}
你可以回想求解一維擴散方程時,步驟3離散二階微分項的方法。我們將會使用同樣計算方式,時間項與兩項二階偏微分導數採用前向差分,可得如下式子:
\frac{u_{i,j}^{n+1} - u_{i,j}^n}{\Delta t} = \nu \frac{u_{i+1,j}^n - 2 u_{i,j}^n + u_{i-1,j}^n}{\Delta x^2} + \nu \frac{u_{i,j+1}^n-2 u_{i,j}^n + u_{i,j-1}^n}{\Delta y^2}
與先前一樣,我們重新調整方程式來求解u_{i,j}^{n+1}:
u_{i,j}^{n+1} = u_{i,j}^n + \frac{\nu \Delta t}{\Delta x^2}(u_{i+1,j}^n - 2 u_{i,j}^n + u_{i-1,j}^n) + \frac{\nu \Delta t}{\Delta y^2}(u_{i,j+1}^n-2 u_{i,j}^n + u_{i,j-1}^n)
import numpy
from matplotlib import pyplot, cm
from mpl_toolkits.mplot3d import Axes3D ##library for 3d projection plots
%matplotlib inline###variable declarations
nx = 31
ny = 31
nt = 17
nu = .05
dx = 2 / (nx - 1)
dy = 2 / (ny - 1)
sigma = .25
dt = sigma * dx * dy / nu
x = numpy.linspace(0, 2, nx)
y = numpy.linspace(0, 2, ny)
u = numpy.ones((ny, nx)) # create a 1xn vector of 1's
un = numpy.ones((ny, nx))
###Assign initial conditions
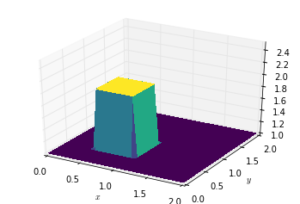
# set hat function I.C. : u(.5<=x<=1 && .5<=y<=1 ) is 2
u[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2 fig = pyplot.figure()
ax = fig.gca(projection='3d')
X, Y = numpy.meshgrid(x, y)
surf = ax.plot_surface(X, Y, u, rstride=1, cstride=1, cmap=cm.viridis,
linewidth=0, antialiased=False)
ax.set_xlim(0, 2)
ax.set_ylim(0, 2)
ax.set_zlim(1, 2.5)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$');u_{i,j}^{n+1} = u_{i,j}^n + \frac{\nu \Delta t}{\Delta x^2}(u_{i+1,j}^n - 2 u_{i,j}^n + u_{i-1,j}^n) + \frac{\nu \Delta t}{\Delta y^2}(u_{i,j+1}^n-2 u_{i,j}^n + u_{i,j-1}^n)
###Run through nt timesteps def diffuse(nt): u[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2 for n in range(nt + 1): un = u.copy() u[1:-1, 1:-1] = (un[1:-1,1:-1] + nu * dt / dx**2 *(un[1:-1, 2:] - 2 * un[1:-1, 1:-1] + un[1:-1, 0:-2]) + nu * dt / dy**2 * (un[2:,1: -1] - 2 * un[1:-1, 1:-1] + un[0:-2, 1:-1])) u[0, :] = 1 u[-1, :] = 1 u[:, 0] = 1 u[:, -1] = 1 fig = pyplot.figure() ax = fig.gca(projection='3d') surf = ax.plot_surface(X, Y, u[:], rstride=1, cstride=1, cmap=cm.viridis, linewidth=0, antialiased=True) ax.set_zlim(1, 2.5) ax.set_xlabel('$x$') ax.set_ylabel('$y$');
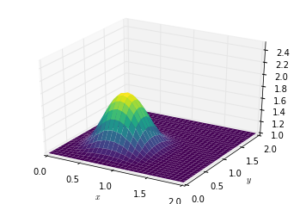
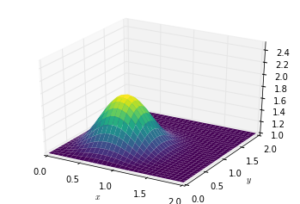
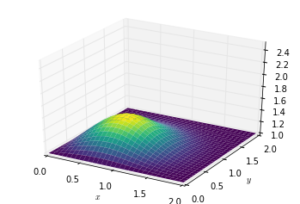
diffuse(10)diffuse(14)diffuse(50)參考資料
- 12 steps to Navier–Stokes: Step 7: 2D Diffusion,Lorena A. Barba

本著作係採用創用 CC 姓名標示 4.0 國際 授權條款授權.